Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 3 2022
Vì AC//CD =>\(\dfrac{OA}{AB}=\dfrac{OC}{CD}\Leftrightarrow\dfrac{2}{3}=\dfrac{3}{CD}\Leftrightarrow CD=\dfrac{3.3}{2}=4,5cm\)
CM
6 tháng 12 2017
a) Chỉ ra điểm O nằm giữa hai điểm B và A. Từ đó tính được AB = 5 cm.
b) Chỉ ra điểm B nằm giữa hai điểm A và C. Từ đó tính được AC = 10 cm.
CM
25 tháng 10 2018
a) Do A; B cùng thuộc tia Ox; OA < OB ( 2cm < 5cm) nên A nằm giữa O và B.
Khi đó : OB = OA + AB
AB = OB - OA = 5 - 2 = 3 (cm)
C nằm trên tia đối của tia OA nên O nằm giữa A và C
AC = CO + OA = 1 + 2 = 3 (cm)
AB = 3 cm ; AC = 3 cm
16 tháng 5 2016
bạn tự vẽ hình nha
a)xét tam giác AOC và tam giác BOC
có +OB=OA(gt)
+\(O_1=O_2\) (Ot là tia phân giác của góc xOy)
+OC: cạnh chung
vậy tam giác AOC= tam giác BOC
b) vì tam giác AOC=tam giácBOC(CMT)
=>AC=CB(2 góc tương ứng)
do đó CO là tiaa phân giác của góc ACB
CM
15 tháng 7 2018
a) Do A; B cùng thuộc tia Ox; OA < OB ( 2cm < 5cm) nên A nằm giữa O và B.
Khi đó : OB = OA + AB
AB = OB - OA = 5 - 2 = 3 (cm)
C nằm trên tia đối của tia OA nên O nằm giữa A và C
AC = CO + OA = 1 + 2 = 3 (cm)
AB = 3 cm ; AC = 3 cm
b) Ta có: A nằm giữa B và C
AB = AC = 3 cm
⇒ Điểm A là trung điểm của đoạn thẳng BC.
CM
11 tháng 7 2019
a) Chỉ ra điểm O nằm giữa hai điểm A và B. Từ đó tính được AB = 7 cm.
b) Chỉ ra điểm C nằm giữa hai điểm O và B. Từ đó tính được BC = 2 cm. Tương tự, tính được AC = 9 cm.
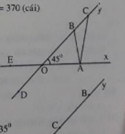
Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D hay AC // BD.
Áp dụng định lí Thalès vào tam giác OBD, ta có:
\(\dfrac{{OA}}{{OB}} = \dfrac{{OC}}{{O{\rm{D}}}}\) hay \(\dfrac{2}{5} = \dfrac{3}{{O{\rm{D}}}}\)
Suy ra: \(O{\rm{D}} = \dfrac{{5.3}}{2} = 7,5(cm)\)
Ta có OD = OC + CD suy ra CD = OD – OC = 7,5 – 3 = 4,5 (cm).
Vậy CD = 4,5 cm.