Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


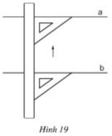
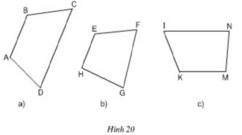
Đặt ê ke như hình vẽ để kiểm tra xem mỗi tứ giác có hay không hai cạnh song song.
+ Tứ giác ABCD có AB // CD nên là hình thang.
+ Tứ giác EFGH không có hai cạnh nào song song nên không phải hình thang.
+ Tứ giác KMNI có KM // IN nên là hình thang.

- Ta kiểm tra các cặp cạnh đối xem chúng có bằng nhau không
Nếu các cặp cạnh đối bằng nhau ⇒ ABCD là hình bình hành
- Sau đó: Kiểm tra hai đường chéo xem chúng bằng nhau không
Nếu hai đường chéo bằng nhau ⇒ ABCD là hình chữ nhật

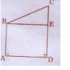
- Học sinh dùng ê – ke vẽ như hình dưới
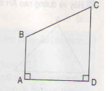
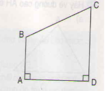
- Học sinh dùng ê – ke để kiểm tra sẽ thấy góc đỉnh E của tứ giá BEDA là góc vuông
Nói thêm: Góc đỉnh B của tứ giác đó cũng là góc vuông. Tứ giác ABDA là hình chữ nhật

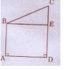
- Học sinh dùng ê – ke vẽ như hình dưới
- Học sinh dùng ê – ke để kiểm tra sẽ thấy góc đỉnh E của tứ giá BEDA là góc vuông
Nói thêm: Góc đỉnh B của tứ giác đó cũng là góc vuông. Tứ giác ABDA là hình chữ nhật

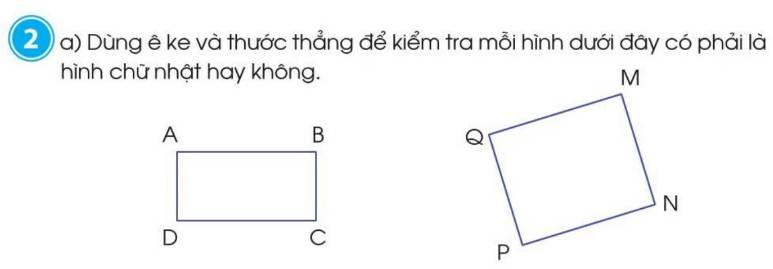
a) Dùng thước ê ke kiểm tra các góc của hai hình:
- Hình ABCD có bốn góc A, B, C và D đều là góc vuông nên hình ABCD là hình chữ nhật.
- Hình MNPQ có bốn góc M, N, P và Q đều là góc vuông nên hình MNPQ là hình chữ nhật.
b) Đo độ dài các cạnh của mỗi hình chữ nhật, ta có:
- Hình chữ nhật ABCD có AB = CD = 3 cm; AD = BC = 2 cm.
- Hình chữ nhật MNPQ có MQ = NP = 30 mm; MN = PQ = 25 mm.

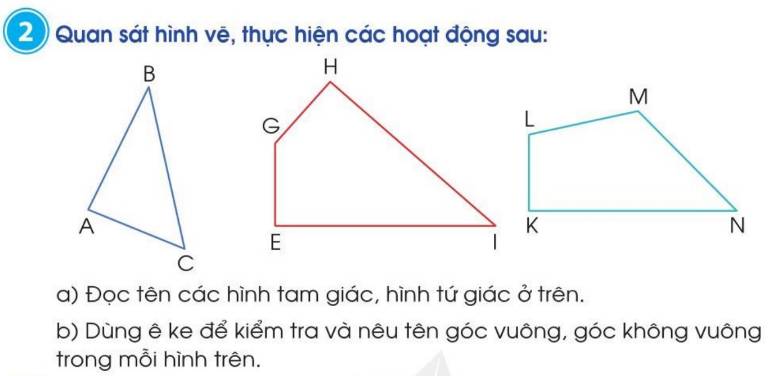
a) Hình tam giác ABC, hình tứ giác EGHI, hình tứ giác KLMN.
b)
Hình tam giác ABC có góc vuông đỉnh A, cạnh AB và AC.
Hình tứ giác GHIE có góc vuông đỉnh E, cạnh EG và EI; góc vuông đỉnh H, cạnh HG và HI.
Hình tứ giác KLMN có góc vuông đỉnh K cạnh KL và KN.

Dùng ê ke kiểm tra bốn góc của tứ giác đó:
• Nếu bốn góc của tứ giác đều là góc vuông thì tứ giác đó là hình chữ nhật;
• Nếu bốn góc của tứ giác có ít nhất một góc không vuông thì tứ giác đó không là hình chữ nhật.
Giải thích: Hình chữ nhật là tứ giác có bốn góc vuông.