Xét đơn thức \(2{{\rm{x}}^3}{y^4}\). Trong các đơn thức này, biến x, y được viết bao nhiêu lần dưới dạng một lũy thừa với số mũ nguyên dương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
H9
HT.Phong (9A5)
CTVHS
13 tháng 10 2023
a) \(\dfrac{9}{4}-3y+y^2\)
\(=\left(\dfrac{3}{2}\right)^2-3y+y^2\)
\(=y^2-2\cdot\dfrac{3}{2}\cdot y+\left(\dfrac{3}{2}\right)^2\)
\(=\left(y-\dfrac{3}{2}\right)^2\)
b) \(x^3+6x^2y+12xy^2+8y^3\)
\(=x^3+6x^2y+12xy^2+\left(2y\right)^3\)
\(=x^3+3\cdot x^2\cdot2y+3\cdot x\cdot\left(2y\right)^2+\left(2y\right)^3\)
\(=\left(x+2y\right)^2\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2023
Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn nhé.
VP
1
21 tháng 2 2017
* \(B=64x^6y^{12}=4^3x^{2\times3}y^{4\times3}=4^3\times\left(x^2\right)^3\times\left(y^4\right)^3=\left(4x^2y^4\right)^3\)
Vậy đơn thức \(B=64x^6y^{12}\) được viết dưới dạng lũy thừa của một đơn thức là \(\left(4x^2y^4\right)^3.\)
* \(B=64x^6y^{12}=2^6x^6y^{12}=2^6x^6y^{2\times6}=2^6x^6\times\left(y^2\right)^6=\left(2xy^2\right)^6\)
Vậy đơn thức \(B=64x^6y^{12}\) được viết dưới dạng lũy thừa của một đơn thức là \(\left(2xy^2\right)^6\).
* \(B=64x^6y^{12}=8^2x^6y^{12}=8^2x^{3\times2}y^{6\times2}=8^2\times\left(x^3\right)^2\times\left(y^6\right)^2=\left(8x^3y^6\right)^2\)
Vậy đơn thức \(B=64x^6y^{12}\) được viết dưới dạng lũy thừa của một đơn thức là \(\left(8x^3y^6\right)^2\).
* \(B=64x^6y^{12}=\left(-8\right)^2x^6y^{12}=\left(-8\right)^2x^{3\times2}y^{6\times2}=\left(-8\right)^2\times\left(x^3\right)^2\times\left(y^6\right)^2=\left(-8x^3y^6\right)^2\)
Vậy đơn thức \(B=64x^6y^{12}\) được viết dưới dạng lũy thừa của một đơn thức là \(\left(-8x^3y^6\right)^2\).
....Và còn nhiều đáp án khác.... 
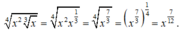
Đơn thức \(2{{\rm{x}}^3}{y^4}\) các biến x, y được viết một lần dưới dạng lũy thừa với số mũ nguyên dương.