Chỉnh sửa các chi tiết để có thể áp dụng chương trình phân tích kết quả học tập theo các quy định của trường em.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


marks = []
line = input("Hãy nhập các điểm kiểm tra cách nhau bởi dấu cách: ")
marks = [float(x) for x in line.split()]
total = 0
min_mark = marks[0]
max_mark = marks[0]
for m in marks:
total += m
if min_mark > m:
min_mark = m
if max_mark < m:
max_mark = m
#a) Thông báo điểm đầu tiên và điểm cuối cùng trong danh sách.
print("Điểm trung bình: ", total / len(marks))
print("Điểm cao nhất: ", max_mark)
print("Điểm thấp nhất: ", min_mark)
print("Điểm đầu tiên: ", marks[0])
print("Điểm cuối cùng: ", marks[-1])
#b)Cho phép người dùng tra cứu đầu điểm thứ n với quy ước n bắt đầu từ 1 ứng với điểm đầu tiên, nếu n lớn hơn tổng số đầu điềm hoặc nhỏ hơn 1, cần thông báo không hợp lệ và yêu cầu người dùng nhập lại.
while True:
try:
n = int(input("Nhập n để tra cứu điểm đầu tiên thứ n (n bắt đầu từ 1): "))
if n < 1 or n > len(marks):
print("Số n không hợp lệ. Vui lòng nhập lại.")
continue
print("Điểm đầu tiên thứ", n, "là:", marks[n - 1])
break
except ValueError:
print("Số n không hợp lệ. Vui lòng nhập lại.")

Nếu bn trả lời câu hỏi dạng mới thì các bn ấy vẫn trả lời được mà

program b1;
uses crt;
var i,n,dat,chuadat:integer;
a:array[1..100] of integer;
begin
clrscr;
write('Nhap tong so ban trong lop:');
readln(n);
for i:=1 to n do readln(a[i]);
dat:=0; chuadat:=0;
for i:=1 to n do
begin
if (a[i]>=5) then inc(dat);
if (5>=a[i]) then inc(chuadat);
end;
writeln('So hoc sinh dat la:',dat);
writeln('So hoc sinh chuadat la:',chuadat);
readln;
end.
Tham khao!

Tham khảo:
Giai đoạn 1. Liệt kê các việc lớn để nhận được các kết quả KQ1, KQ2 và KQ3 1. Đọc dữ liệu từ tập Tổ chức dữ liệu trong chương trình bằng các kiểu dữ liệu của Python sao cho thuận tiện để thực hiện các việc tiếp theo,
2. Phân tích dãy điểm từng học sinh để có KQI và KQ3; viết kết quả vào các tập “phantich_theoHS.txt", "xetKhenThuong tri
3. Với mỗi môn học, sắp xếp dãy điểm để có KQ2a, viết kết quả vào tệp “phantich_
theoMon.txt";
4. Với mỗi môn học, phân tích dãy điểm để có KQ2b; viết kết quả vào tệp "phantich
theoMon.txt".
Giai đoạn 2. Thiết kế các hàm
1. Đọc dữ liệu từ tập
Dữ liệu đầu vào chứa trong một tệp, dọc vào từng dòng và xử lí không phức tạp. Có thể viết một hàm thực hiện việc này. Đặt tên hàm: ví dụ là nhapTuTep.
Đầu vào: tập phần mềm bảng tính chứa dữ liệu như mô tả ở đầu bài học. Đầu ra: dữ liệu trong chương trình được tổ chức như sau:
- Mảng hai chiều các điểm số: Mảng nx m, mỗi hàng là dãy điểm của một học sinh, sẵn sàng để phân tích kết quả cho từng học sinh.
- Cột Tên trong bảng kết quả học tập tạo thành danh sách các tên học sinh để ghép với từng cột điểm số môn học, tách riêng được kết quả học tập theo từng môn.
– Hàng các tên môn học tạo thành danh sách tên môn học để dễ dàng lấy ra từng tên môn học theo chỉ số cột.
2. Phân tích điểm theo học sinh
Có thể tách thành các việc nhỏ, cụ thể hơn như sau:
2a) Phân tích dãy điểm số (là một hàng của mảng hai chiều) để có KQI: Thiết kế một hàm và đặt tên, ví dụ là ptDiem
Đầu vào: một dãy điểm số
Đầu ra: trả về sum, max, min, số lượng điểm thuộc các mức xếp hạng Tốt, Khá
Dat, Chura dat.
2b) Xét khen thưởng
Nếu chamDiem > 0 thì viết thêm (tên, chamDiem) thành một dòng vào tập “xetKhenThuong.txt"; có thể thực hiện việc này bằng một vài câu lệnh ngắn gọn, không cần viết thành một hàm riêng.
Lặp lại các việc 2a) và 2b) cho mỗi hàng trong mảng hai chiều axim sẽ hoàn thành phân tích điểm cho toàn bộ học sinh và lập xong danh sách học sinh được xét khen thưởng.
Có thể thiết kế thân vòng lặp thành một hàm và đặt tên, ví dụ là ptHocSinh.
Đầu vào: Một hàng trong mảng hai chiều axim (một dãy điểm số).
Dau ra
- Thêm một dòng vào tập “phantich theoHS.txt" (gọi hàm ptDiem) — Thêm (tên, chamliem) vào tập “xetKhenThuong.txt" nếu chamDiem ≥ 0, 3. Phân tích điểm theo môn học
3a) Chuẩn bị đầu vào để sẵn sàng phân tích điểm theo môn học:
Dãy điểm số một môn học là một cột của mảng hai chiều năm không sẵn có ngayn như một danh sách Phython. Cũng chưa có sẵn danh sách các cặp (tên, điểm) là kết quả của mỗi môn học (ở đây tên là tên học sinh).
Thiết kế một hàm, đặt tên ví dụ là tach Mom
- Đầu vào: dữ liệu trong chương trình (sau khi đọc từ tập vào)
- Đầu ra: trả về tên danh sách dãy điểm số một môn học và tên danh sách các cặp (tên, điểm) cho môn học đó.
3b) Phân tích điểm một môn học.
Nhận thấy rằng yêu cầu kết quả đầu ra KQI và KQ28 là tương tự như nhau. Hàm ptlhiem sử dụng được cho cả hai việc, phân tích điểm từng học sinh và phân tích điểm từng môn học.
3c) Sắp xếp danh sách các cặp (tên, điểm) theo thứ tự điểm giảm dần để có KQ2a.
Ta đã viết một số chương trinh thực hiện các thuật toán sắp xếp dãy số. Có thể cải biên để nhận được một hàm thực hiện sắp xếp danh sách các cặp (tên, điểm) theo thứ tự điểm giảm dần.
Lặp lại các việc 3h) và 30) cho mỗi cột trong mảng hai chiều a x m sẽ hoàn thành phân tích điểm cho toàn bộ các môn học. Có thể thiết kế một hàm nhận kết quả từ tach Mon và thực hiện 3b) và 3c) cho một môn học; đặt tên, ví dụ là ptMonHoc. - Đầu vào: danh sách điểm một môn học và danh sách các cặp (tên, điểm).
- Đầu ra:
+Thêm một dòng vào tập “phantich_theoMon.txt" (gọi hàm ptDiem). +Thêm danh sách các cặp (tên, điểm) theo thứ tự điểm giảm dần vào tập “phantich theoMon.txt" (gọi hàm sắp xếp đã cải biển).


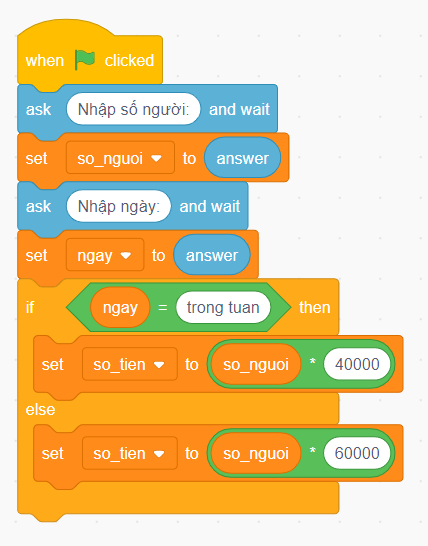
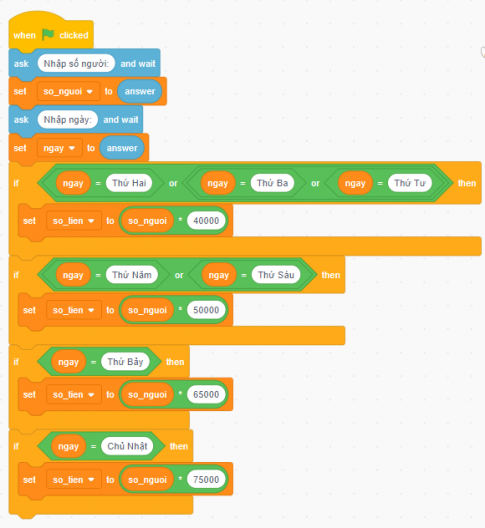

Học sinh phân tích và tiến hành chỉnh sửa các chi tiết để có thể áp dụng chương trình phân tích.