Cho hình vuông ABCD. Trên tia đối của tia CD lấy điểm E bất kì sao cho CE<CD. Kẻ BM vuông góc với BE (M ϵ BE), BM cắt BC tại H, AH cắt BD tại I, AC cắt BD tại O. a) Chứng minh rằng EI vuông góc với BD. b) Chứng minh rằng MI là tia phân giác của góc BMD. c) Tìm vị trí điểm E sao cho tam giác AMD có diện tích lớn nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 4 2018
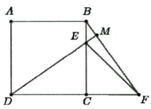
Chứng minh được:
C B F ^ + B E M ^ = M D F ^ + D E C ^ = 90 0
=> B M D ^ = 90 0 nên M thuộc đường tròn đường kính BD. Mà E Î BC nên quỹ tích của điểm M là là cung B C ⏜ của đường tròn đường kính BD
TT
17 tháng 12 2020
a/ \(\widehat{DCE}+\widehat{ECF}=180^o\)
=> \(\widehat{ECF}=90^o\)
Xét t/g DEC và t/g BFC có
EC = FC (GT)
\(\widehat{DCE}=\widehat{BCF}=90^o\)
DC = BC (do ABCD là hình vuông)
=> t/g DEC = t/g BFC (c.g.c)
=> DE = BF (2 cạnh t/ứ(
b/ Xét t/g BEH và t/g DEC có
\(\widehat{BEH}=\widehat{DEC}\) (đối đỉnh)
\(\widehat{EBF}=\widehat{EDC}\) (do t/g BFC = t/g DEC)
\(\Rightarrow\Delta BEH\sim\Delta DEC\) (g.g)
=> \(\widehat{BHE}=\widehat{DCB}=90^o\)
=> \(DE\perp BF\)
Xét t/g BDF có
DE ⊥ BF
BC ⊥ DF
DE cắt BC tại E
=> E là trực tâm t/g BDF
=> .... đpcm
c/ Xét t/g CEF có CE = CF ; M là trung điểm EF
=> CM ⊥ EF
=> \(\widehat{KMC}=90^o\)
Tự cm OKMC làhcn
=> OC = KM => AO = KM
Mà AO // KM (cùng vuông góc vs BD)
=> AOMK là hbh
=> OM // AK
9 tháng 5 2020
Xét tứ giác CDNB có \(\widehat{DNB}+\widehat{BCD}=90^o+90^o=180^o\) nên là tứ giác nội tiếp ( 1 )
Xét tứ giác ANBD có \(\widehat{DAB}=\widehat{DNB}=90^o\)nên là tứ giác nội tiếp ( 2 )
Từ ( 1 ) và ( 2 ) suy ra 5 điểm A,N,B,C,D cùng thuộc 1 đường tròn
suy ra tứ giác ANCD nội tiếp đường tròn
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)
