Mô phỏng chi tiết các bước lặp sắp xếp chèn dãy A = [5, 0, 4, 2, 3]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


*Thuật toán sắp xếp chèn (Insertion Sort):
import time
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp chèn
insertion_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là 0 giây
*Thuật toán sắp xếp chọn:
import time
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp chọn
selection_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là: 0 giây
*Thuật toán sắp xếp nổi bọt:
import time
def bubble_sort(arr):
n = len(arr)
for i in range(n - 1):
for j in range(n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
# Dãy số nguyên đầu vào
A = [3, 1, 0, 10, 13, 16, 9, 7, 5, 1]
# In dãy số nguyên trước khi sắp xếp
print("Dãy số nguyên trước khi sắp xếp:", A)
# Bắt đầu đo thời gian thực hiện thuật toán
start_time = time.time()
# Gọi hàm sắp xếp nổi bọt
bubble_sort(A)
# Kết thúc đo thời gian thực hiện thuật toán
end_time = time.time()
# In dãy số nguyên sau khi sắp xếp
print("Dãy số nguyên sau khi sắp xếp:", A)
# In thời gian thực hiện thuật toán
print("Thời gian thực hiện thuật toán: {:.6f} giây".format(end_time - start_time))
Thời gian thực hiện là: 0 giây

- Bước 1: i = 0;
- Bước 2: Tìm phần tử a[min] nhỏ nhất trong dãy hiện hành từ a[i] đến a[n-1].
- Bước 3: Đổi chỗ a[min] và a[i].
- Bước 4: Nếu i < n-1 thì gán i = i+1; rồi lặp lại bước 2, ngược lại -> Dừng.

THAM KHẢO!
1.Thuật toán sắp xếp chèn (Insertion Sort):
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
A = [5, 8, 1, 0, 10, 4, 3]
sorted_A = insertion_sort(A)
print("Dãy A sau khi sắp xếp chèn:", sorted_A)
2. Thuật toán sắp xếp chọn (Selection Sort):
def selection_sort(arr):
for i in range(len(arr)):
min_idx = i
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr
A = [5, 8, 1, 0, 10, 4, 3]
sorted_A = selection_sort(A)
print("Dãy A sau khi sắp xếp chọn:", sorted_A)
3.Thuật toán sắp xếp nổi bọt (Bubble Sort):
def bubble_sort(arr):
n = len(arr)
for i in range(n - 1):
for j in range(n - 1 - i):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
A = [5, 8, 1, 0, 10, 4, 3]
sorted_A = bubble_sort(A)
print("Dãy A sau khi sắp xếp nổi bọt:", sorted_A)

- Bắt đầu từ vị trí đầu tiên của danh sách (bên trái), so sánh các cặp số với nhau, nếu không đúng thứ tự nhỏ-lớn thì đảo vị trí.
- Sau khi chạy tới cuối danh sách, tiếp tục chạy lại từ vị trí đầu danh sách cho đến khi hoàn thành so sánh và đảo vị trí.

#include <bits/stdc++.h>
using namespace std;
long long a,b;
int main()
{
cin>>a>>b;
cout<<a<<" "<<b<<endl;
swap(a,b);
cout<<a<<" "<<b;
return 0;
}

Ý tưởng của thuật toán sắp xếp chèn là thực hiện vòng lặp duyệt từ phần tử thứ hai đến cuối dãy. Sau mỗi bước lặp phần tử tương ứng sẽ được chèn vào vị trí đúng của dãy con đã sắp xếp là các phần tử phía trước vị trí đang duyệt.

#include <bits/stdc++.h>
using namespace std;
long long a[1000],n,i,tam,j;
int main()
{
cin>>n;
for (i=1; i<=n; i++)
cin>>a[i];
for (i=1; i<=n-1; i++)
for (j=i+1; j<=n; j++)
if (a[i]>a[j]) swap(a[i],a[j]);
for (i=1; i<=n; i++)
cout<<a[i]<<" ";
return 0;
}

1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.

2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
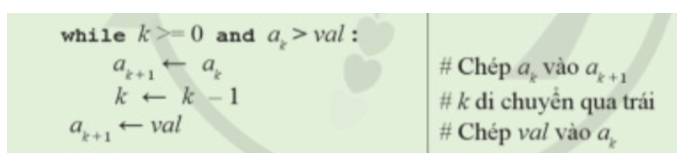
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:
Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.
Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1

#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
sort(a+1,a+n+1);
for (i=1; i<=n; i++) cout<<a[i]<<" ";
return 0;
}

Bước 1: i = 1;//giả sử có đoạn a[0] đã được sắp xếp
Bước 2: x = a[i];
Bước 3:
Tìm vị trí pos thích hợp trong đoạn a[0] đến a[i-1] để chèn a[i] vào danh sách.
Dời chỗ các phần tử từ a[pos] đến a[i-1] sang phải 1 vị trí để dành chổ cho a[i].
Bước 4: a[pos] = x;//chèn x, có đoạn a[0],…,a[i] đã được sắp.
Bước 5: i = i+1; nếu i < n -> lặp lại bước 2, ngược lại -> Dừng.