Cho ∆ABC vuông tại a . Giải ∆ABC , biết , AC = 12cm , góc ABC = 36°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=5^2+12^2=169\)
=>\(BC=\sqrt{169}=13\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{5}{13}\)
nên \(\widehat{B}\simeq23^0\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}\simeq90^0-23^0=67^0\)
b: Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-40^0=50^0\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(BC=\dfrac{AC}{sinB}=\dfrac{5}{sin40}\simeq7,78\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB^2=BC^2-AC^2\)
=>\(AB\simeq\sqrt{7,78^2-5^2}\simeq5,96\left(cm\right)\)

BH=12^2/9=16cm
BC=16+9=25cm
AB=căn(16*25)=20cm
AC=căn(9*25)=15cm
sin B=AC/BC=3/5
tan C=AB/AC=20/15=4/3

Áp dụng định lí Pytago vào tam giác ABC ta có:
B C 2 = A B 2 + A C 2 suy ra: A B 2 = B C 2 - A C 2 = 20 2 - 12 2 = 256
Nên AB = 16cm
* Xét tam giác AHB và tam giác CAB có:
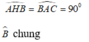
Suy ra: Δ AHB và CAB đồng dạng ( g.g) .
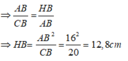
Chọn đáp án D

\(\widehat{C}=60^0\)
BC=24cm
\(AC=12\sqrt{3}\left(cm\right)\)

ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}+30^0=90^0\)
=>\(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{12}=sin30=\dfrac{1}{2}\)
=>AB=6(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=144-36=108\)
=>\(AC=6\sqrt{3}\left(cm\right)\)
ABC vuông tại A
⇒ ∠B + ∠C = 90⁰
⇒ ∠B = 90⁰ - ∠C
= 90⁰ - 30⁰
= 60⁰
sinB = AC/BC
⇒ AC = BC . sinB
= 12 . sin60⁰
= 6√3 (cm)
sinC = AB/BC
⇒ AB = BC.sinC
= 12.sin30⁰
= 6 (cm)