không cần làm câu a b c đâu ạ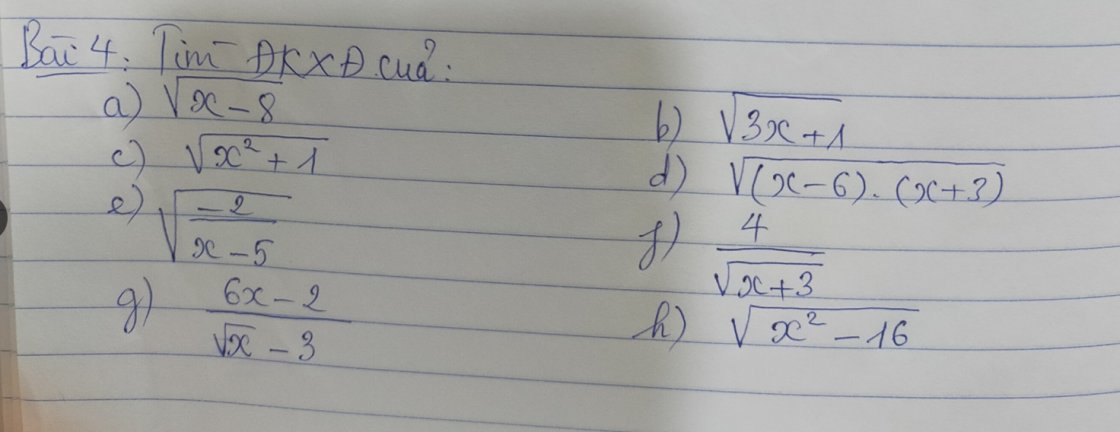
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2:
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp

\(2,\Leftrightarrow\left\{{}\begin{matrix}20x+25y-10xy=0\\20x-30y+xy=0\end{matrix}\right.\Leftrightarrow55y-11xy=0\\ \Leftrightarrow11y\left(5-x\right)=0\Leftrightarrow\left[{}\begin{matrix}y=0\\x=5\end{matrix}\right.\)
Với \(y=0\Leftrightarrow4x+0=0\Leftrightarrow x=0\)
Với \(x=5\Leftrightarrow20+5y=10y\Leftrightarrow y=4\)
Vậy \(\left(x;y\right)=\left\{\left(0;0\right);\left(5;4\right)\right\}\)

12) \(4C_xH_y\left(COOH\right)_2+\left(2x+y+2\right)O_2\xrightarrow[]{t^o}\left(4x+8\right)CO_2+\left(2y+4\right)H_2O\)
13) \(2KHCO_3+Ca\left(OH\right)_2\rightarrow K_2CO_3+CaCO_3+2H_2O\)
14) \(Al_2O_3+6KHSO_4\rightarrow Al_2\left(SO_4\right)_3+3K_2SO_4+3H_2O\)
15) \(xFe_2O_3+\left(3x-2y\right)H_2\xrightarrow[]{t^o}2Fe_xO_y+\left(3x-2y\right)H_2O\)


Khi hỏi người lớn tuổi, các em cần chú ý những điểm sau:
+ Chú ý cách xưng hô phù hợp, lịch sự
+ Thể hiện được sự lễ phép, văn minh.
+ Bộc lộ được mục đích lời hỏi
Em nên dùng cách hỏi: " Bác có thể chỉ giúp cháu bưu điện ở đâu không ạ?

b6 fashion - long hours - contacted - clients - grades
b5 c làm ở dưới r í

Câu b bạn tự vẽ
Câu c:
PT hoành độ giao điểm: \(-3x+1=\left(1-2m\right)x+m-1\)
Mà 2 đt cắt tại hoành độ 1 nên \(x=1\)
\(\Leftrightarrow-2=1-2m+m-1\Leftrightarrow m=2\)
Câu d:
PT giao Ox,Oy lần lượt tại A,B của (d) là:
\(\left\{{}\begin{matrix}y=0\Rightarrow x=\dfrac{m-1}{2m-1}\Rightarrow A\left(\dfrac{m-1}{2m-1};0\right)\Rightarrow OA=\left|\dfrac{m-1}{2m-1}\right|\\x=0\Rightarrow y=m-1\Rightarrow B\left(0;m-1\right)\Rightarrow OB=\left|m-1\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến (d)
Đặt \(OH^2=t\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m-1\right)^2}{\left(m-1\right)^2}+\dfrac{1}{\left(m-1\right)^2}\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{4m^2-4m+2}{\left(m-1\right)^2}\Leftrightarrow t=\dfrac{m^2-2m+1}{4m^2-4m+2}\\ \Leftrightarrow4m^2t-4mt+2t=m^2-2m+1\\ \Leftrightarrow m^2\left(4t-1\right)+2m\left(1-2t\right)+2t-1=0\)
Coi đây là PT bậc 2 ẩn m, PT có nghiệm
\(\Leftrightarrow\Delta'=\left(1-2t\right)^2-\left(4t-1\right)\left(2t-1\right)\ge0\\ \Leftrightarrow4t^2-4t+1-8t^2+6t-1\ge0\\ \Leftrightarrow2t-4t^2\ge0\\ \Leftrightarrow2t\left(1-2t\right)\ge0\\ \Leftrightarrow0\le t\le\dfrac{1}{2}\)
\(\Leftrightarrow OH^2\le\dfrac{1}{2}\Leftrightarrow OH\le\dfrac{1}{\sqrt{2}}\)
Dấu \("="\Leftrightarrow\dfrac{m^2-2m+1}{4m^2-4m+2}=\dfrac{1}{2}\Leftrightarrow4m^2-4m+2=2m^2-4m+2\)
\(\Leftrightarrow2m^2=0\Leftrightarrow m=0\)
Vậy m=0 thỏa yêu cầu đề
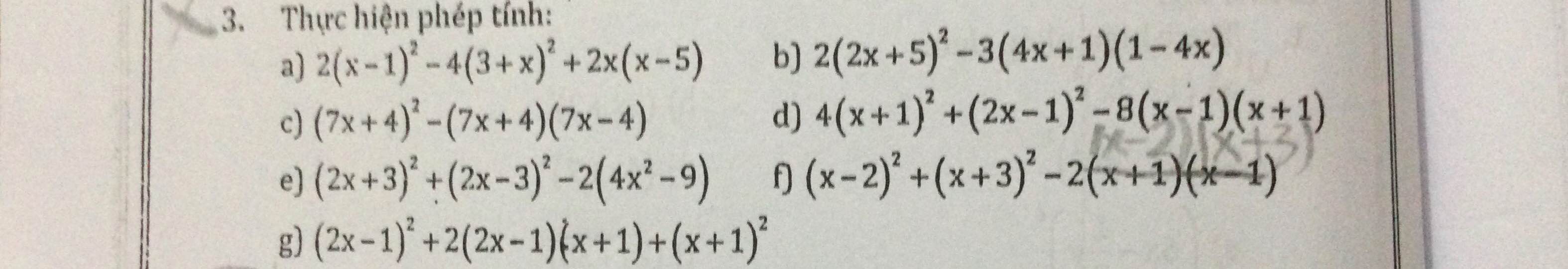 Không cần phải làm câu a,e,f đâu ạ
Không cần phải làm câu a,e,f đâu ạ  không cần làm câu c đâu ạ, giúp e với nhaaa mn
không cần làm câu c đâu ạ, giúp e với nhaaa mn không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ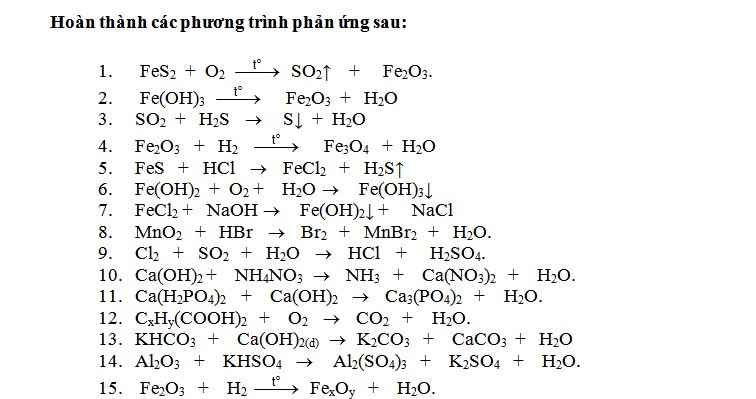







a) \(\sqrt{x-8}\) xác định khi
\(x-8\ge0\Leftrightarrow x\ge8\)
b) \(\sqrt{3x+1}\) xác định khi
\(3x+1\ge0\Leftrightarrow3x\ge-1\Leftrightarrow x\le-\dfrac{1}{3}\)
c) \(\sqrt{x^2+1}\)
Ta có: \(x^2\ge0\Rightarrow x^2+1\ge0\)
Vậy biểu thức được xác định với mọi x
d) \(\sqrt{\left(x-6\right)\left(x+3\right)}\)
Xác định khi
\(\left\{{}\begin{matrix}\left\{{}\begin{matrix}x-6\ge0\\x+3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-6< 0\\x+3\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}x\ge6\\x\ge-3\end{matrix}\right.\\\left\{{}\begin{matrix}x< 6\\x< -3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge6\\x< -3\end{matrix}\right.\)
e) \(\sqrt{\dfrac{-2}{x-5}}\) xác định khi
\(\left\{{}\begin{matrix}\dfrac{-2}{x-5}\ge0\\x-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le5\\x\ne5\end{matrix}\right.\)
\(\Leftrightarrow x< 5\)
f) \(\dfrac{4}{\sqrt{x+3}}\) xác định khi
\(x+3>0\)
\(\Leftrightarrow x>-3\)
g) \(\dfrac{6x-2}{\sqrt{x}-3}\)
Xác định khi:
\(\left\{{}\begin{matrix}\sqrt{x}\ge0\\\sqrt{x}-3\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
h) \(\sqrt{x^2-16}=\sqrt{\left(x+4\right)\left(x-4\right)}\)
Xác định khi
\(\left\{{}\begin{matrix}\left\{{}\begin{matrix}x+4< 0\\x-4< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x+4\ge0\\x-4\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}x< -4\\x< 4\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge-4\\x\ge4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< -4\\x\ge4\end{matrix}\right.\)