Cho hình chóp tứ giác S.ABCD. Gọi I,J lần lượt là trung điểm của SA, SB và M là giao của AC và BD. Chọn khẳng định đúng? A. IJ//(SAB) B. IJ//(MDC) C. IJ//(SDC). D. IJ//(JDC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 7 2018
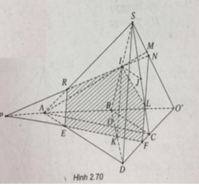
a) Gọi O′ = AB ∩ CD, M = AI ∩ SO′
Ta có: M = AI ∩ (SCD)
b) IJ // BC ⇒ IJ // AD ⇒ IJ // (SAD)
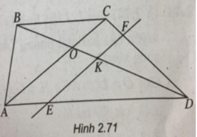
c) Đường thẳng qua I song song với SD cắt BD tại K.
Do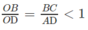 
nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi R = IP ∩ SA. Kéo dài PI cắt SO’ tại N
Gọi L = NF ∩ SC
Ta có thiết diện là ngũ giác IREFL.
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1
a.
Do M là trung điểm SA, O là trung điểm AC
\(\Rightarrow OM\) là đường trung bình tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\) (1)
N là trung điểm CD, O là trung điểm AC \(\Rightarrow ON\) là đường trung bình ACD
\(\Rightarrow ON||AD\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\) (2)
Mà \(ON\cap OM=O\) ; \(OM;ON\in\left(OMN\right)\) (3)
(1);(2);(3) \(\Rightarrow\left(OMN\right)||\left(SBC\right)\)
b.
J cách đều AB, CD \(\Rightarrow J\) thuộc đường thẳng d qua O và song song AB, CD
- Nếu J trùng O \(\Rightarrow OI\) là đường trung bình tam giác SBD \(\Rightarrow OI||SB\Rightarrow OI||\left(SAB\right)\)
Hay \(IJ||\left(SAB\right)\)
- Nếu J không trùng O, ta có \(\left\{{}\begin{matrix}IO||SB\left(đtb\right)\Rightarrow IO||\left(SAB\right)\\d||AB\Rightarrow IJ||AB\Rightarrow OJ||\left(SAB\right)\end{matrix}\right.\)
\(\Rightarrow\left(OIJ\right)||\left(SAB\right)\Rightarrow IJ||\left(SAB\right)\)
4 tháng 1
a.
Do M là trung điểm SA, O là trung điểm AC
là đường trung bình tam giác SAC (1)
N là trung điểm CD, O là trung điểm AC là đường trung bình ACD
(2)
Mà ; (3)
(1);(2);(3)
b.
J cách đều AB, CD thuộc đường thẳng d qua O và song song AB, CD
- Nếu J trùng O là đường trung bình tam giác SBD
Hay
- Nếu J không trùng O, ta có
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 12 2021
a.
Do O là tâm hbh \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow OJ\) là đường trung bình tam giác SAC
\(\Rightarrow OJ||SA\)
Mà \(SA\in\left(SAC\right)\Rightarrow OJ||\left(SAC\right)\)
\(SA\in\left(SAB\right)\Rightarrow OJ||\left(SAB\right)\)
b. O là trung điểm BD, I là trung điểm BC
\(\Rightarrow OI\) là đườngt rung bình tam giác BCD
\(\Rightarrow OI||CD\)
Mà \(CD\in\left(SCD\right)\Rightarrow OI||\left(SCD\right)\)
Tương tự ta có IJ là đường trung bình tam giác SBC \(\Rightarrow IJ||SB\Rightarrow IJ||\left(SBD\right)\)
c. Ta có I là trung điểm BC, O là trung điểm AC
\(\Rightarrow M\) là trọng tâm tam giác ABC
\(\Rightarrow BM=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{1}{3}\)
Theo giả thiết \(SK=\dfrac{1}{2}KD=\dfrac{1}{2}\left(SD-SK\right)\Rightarrow SK=\dfrac{1}{3}SD\)
\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}=\dfrac{BM}{BD}\Rightarrow KM||SB\) (Talet đảo)
\(\Rightarrow MK||\left(SBC\right)\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
\(\Delta SAB,\Delta SAC\) đều \( \Rightarrow AB = {\rm{A}}C = a\)
\(BC = \sqrt {S{B^2} + S{C^2}} = a\sqrt 2 \)
\( \Rightarrow \Delta ABC\) vuông cân tại \(A\)
\(AJ\) là trung tuyến của tam giác \(ABC\)\( \Rightarrow AJ = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBC\) vuông cân tại \(S\) có \(SJ\) là trung tuyến
\( \Rightarrow SJ = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}\)
\(IJ\) là trung tuyến của tam giác \(SAJ\)\( \Rightarrow IJ = \frac{{\sqrt {2\left( {A{J^2} + S{J^2}} \right) - S{A^2}} }}{2} = \frac{a}{2}\)
\(AI = \frac{1}{2}SA = \frac{a}{2};BJ = \frac{1}{2}BC = \frac{a}{2}\)
Xét tam giác \(AIJ\) có: \(A{I^2} + I{J^2} = A{J^2}\)
\( \Rightarrow \Delta AIJ\) vuông tại \(I\)\( \Rightarrow AI \bot IJ \Rightarrow SA \bot IJ\)
\(\Delta SAB\) đều \( \Rightarrow BI = \sqrt {A{B^2} - A{I^2}} = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(BIJ\) có: \(B{J^2} + I{J^2} = B{I^2}\)
\( \Rightarrow \Delta BIJ\) vuông tại \(J\)\( \Rightarrow BJ \bot IJ \Rightarrow BC \bot IJ\)
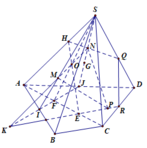
Chọn A