Trong Ví dụ 2, chứng minh rằng đường thẳng c song song với mp(a,b), đường thẳng b song song với mp(a,c).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


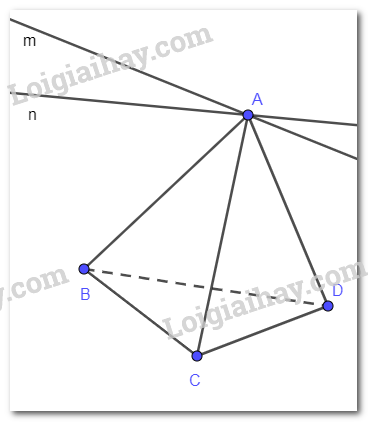
Ta có: m // BC suy ra m // (BCD).
n // BD suy ra n // (BCD).
Mặt phẳng (m,n) chứa hai đường thẳng cắt nhau m và n cùng song song với mặt phẳng (BCD) nên mặt phẳng (m, n) song song với mặt phẳng (BCD).

AD // CF ---> AFCD là hbh ---> AF = CD
DK // BC ---> DKBC là hbh ---> BK = CD
---> AB-AF = AB-BK hay FB = AK (1)
AM // FB ---> ^MAK = ^PFB (góc đồng vị) (2)
MK // PB ---> ^MKA = ^PBF (góc đồng vị) (3)
(1),(2),(3) ---> 2 t/g MAK và PFB bằng nhau (gcg) ---> MA = PF (4)
Mà AC // PF ---> MA // PF (5)
(4),(5) ---> MAFB là hbh ---> MP // AF ---> MP // AB
b)
Gọi Q là giao điểm của MP và CF, B' là giao điểm của DQ và AB ---> B và B' nằm cùng phía đối với đt CF
CD // FB' ---> 2 t/g QCD và QFB' đồng dạng ---> QC/QF = CD/FB' (5)
QP // FB ---> QC/QF = PC/PB (6)
FB // AC ---> PC/PB = FA/FB = CD/FB (7)
(5),(6),(7) ---> FB' = FB
Mà B và B' nằm cùng phía đối với đt CF nên B' trùng B ---> DB đi qua Q hay nói cách khác MP,CF,DB đồng quy tại Q
chà tìm thấy trên mạng :)

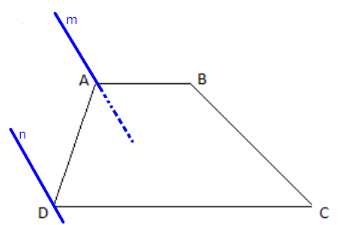
Ta có: m // n suy ra m // (C,n).
Có: AB // CD (do ABCD là hình thang) suy ra AB // (C,n).
Mặt phẳng (B,m) chứa hia đường thẳng cắt nhau m và AB song song với mp(C,n) suy ra (B,m) // (C,n).

a) Do CD // AB, DM // BD nên ta dễ thấy : \(\Delta DMC\)đồng dạng với \(\Delta MCA\left(g.g\right)\)
\(\Rightarrow\frac{MC}{CA}=\frac{CD}{AB}=\frac{AF}{AB}\)( vì ADCF là hình bình hành nên CD = AF ) (1)
Lại có : FP // AC nên : \(\frac{CP}{CB}=\frac{AF}{AB}\left(2\right)\)
Từ (1) và (2) => \(\frac{CM}{CA}=\frac{CP}{CB}\)
Theo định lí Ta-let đảo, ta có : MP // AB
b) Gọi N và N' là giao điểm MP,DB với CF
Ta có : \(\frac{CN}{CF}=\frac{CM}{CA}=\frac{CD}{AB}\)(ở phần a)
\(\frac{CN'}{N'F}=\frac{CD}{FB}\Rightarrow\frac{AN'}{CF}=\frac{CD}{\left(FB+CD\right)}=\frac{CD}{AB}\)( vì CD = AF )
Vậy CN = CN' nên N' trùng N
Từ đó, ta suy ra được : MP, CF, DB đồng quy

a)Kẻ NP
Ta có:
a//b
=> MNP=NPQ(so le trong)
Xét \(_{\Delta MPN}\) và \(\Delta QNP\) có:
MNP=NPQ( cmt)
NP là cạnh chung
MN=QP
=)\(\Delta MNP=\Delta QNP\)(C-g-C)(1)
=>MPN=QNP(hai cạnh tương ứng)
Mà hai góc này ở vị trí so le trong => MP//NQ(dpcm)
b) Từ (1) => MP=NP(dpcm)
CHÚC BẠN HỌC TỐT!
a) ta có a//b suy ra MN//PQ suy ra góc MNP = góc NPQ (hai góc so le trong)
xét tam giác MNP và tam giác QPN ta có
MN=QP
góc MNP= góc QPN
NP:cạnh chung
suy ra tam giác MNP= tam giác QPN(c.g.c)
suy ra MP=NQ(hai cạnh tương ứng)
b)ta có tam giác MNP= tam giác QPN suy ra góc MPN=góc QNP(hai góc tương ứng)
mà hai góc này ở vị trí so le trong suy ra MP//NQ(đpcm)

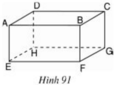
a) Những đường thẳng song song với mặt phẳng (EFGH) là: AB; BC; CD; DA.
b) Đường thẳng AB song song với những mặt phẳng: (CDHG); (EFGH); (DCFE)
c) Đường thẳng AD song song với những đường thẳng: BC, FG, EH

Bạn xem lời giải của cô Huyền ở đường link phía dưới nhé:
Câu hỏi của Edogawa Conan - Toán lớp 8 - Học toán với OnlineMath
Tham khảo link này: https://olm.vn/hoi-dap/detail/81945110314.html
Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên đường thẳng c không nằm trong mp (a, b). Vì đường thẳng c song song song với đường thẳng b và đường thẳng b nằm trong mp (a, b) nên đường thẳng c song song với mp (a, b).
Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên đường thẳng a không nằm trong mp (a, c). Vì đường thẳng b song song song với đường thẳng c và đường thẳng c nằm trong mp (a, c) nên đường thẳng b song song với mp (a, c).