Gia đình nhím có một số thành viên . Biết 2 thành viên nhẹ nhất chiếm 25% tổng cân nặng của cả gia đình , 3 thành viên nặng nhất chiếm 60% tổng cân nặng của cả gia đình . hỏi gia đình nhím có bao nhiêu thành viên ? giải thích
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2 thành viên nhẹ nhất tổng cân 25% cân nặng cả gia đình => Bình quân mỗi TV này nặng 12,5% tổng cân nặng gia đình
3 thành viên năng nhất chiếm 60% tổng cân nặng cả gia đình => Bình quân mỗi TV này nặng 20% tổng cân nặng gia đình
Tổng cân nặng 2TV nhẹ nhất và 3 TV nặng nhất gia đình: 25%+60%=85% (tổng cân nặng cả gia đình)
Vì: 12,5% < 100% - 85% < 20%
Nên ngoài 2TV nhẹ nhất và 3 TV nặng nhất, gia đình chỉ còn duy nhất 1 thành viên
Vậy gia đình đó có:
2+3+1=6(thành viên)

Trong 6 năm tổng số tuổi tăng thêm 120-96=24 tuổi
=>Gia đình có 24/6=4 thành viên

Chọn đáp án C
Trong quan hệ hôn nhân và gia đình, vợ và chồng bình đẳng với nhau, có quyền và nghĩa vụ ngang nhau về mọi mặt trong gia đình, bao gồm quan hệ nhân thân và quan hệ tài sản. Việc làm của anh A là vi phạm cả quan hệ nhân thân và quan hệ tài sản.

Chọn đáp án C
Trong quan hệ hôn nhân và gia đình, vợ và chồng bình đẳng với nhau, có quyền và nghĩa vụ ngang nhau về mọi mặt trong gia đình, bao gồm quan hệ nhân thân và quan hệ tài sản. Việc làm của anh A là vi phạm cả quan hệ nhân thân và quan hệ tài sản.

Gọi số thành viên của mỗi gia đình lần lượt là x, y, z ( người)
Vì số thành viên và thời gian tiêu thụ hết thực phẩm là hai đại lượng tỉ lệ nghịch nên:
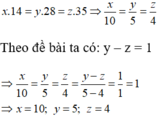
Chọn đáp án C
 đâynhé nhớ tick cho mình nhé bạn
đâynhé nhớ tick cho mình nhé bạn
Giả sử số thành viên trong gia đình nhím là x.
Gọi cân nặng của các thành viên lần lượt là a1, a2, ..., ax.
Theo đề bài, ta có hệ phương trình sau:
a1 + a2 = 0.25(a1 + a2 + ... + ax) (1)
a1 + a2 + a3 = 0.6(a1 + a2 + ... + ax) (2)
Từ (1), ta có:
0.75(a1 + a2) = 0.75(a1 + a2 + ... + ax) (3)
Từ (2), ta có: 0.4(a1 + a2 + a3) = 0.4(a1 + a2 + ... + ax) (4)
Từ (3) và (4), ta có: 0.75(a1 + a2)
= 0.4(a1 + a2 + a3) 0.75a1 + 0.75a2
= 0.4a1 + 0.4a2 + 0.4a3 0.35a1 + 0.35a2
= 0.4a3
Từ đây, ta thấy rằng a1 + a2 phải lớn hơn a3.
Điều này chỉ xảy ra khi a1 + a2 + a3 là số lớn nhất trong tổng cân nặng của gia đình nhím.
Vậy, ta có thể kết luận rằng số thành viên trong gia đình nhím là 3.
Giả sử số thành viên trong gia đình nhím là x.
Gọi cân nặng của các thành viên lần lượt là a1, a2, ..., ax.
Theo đề bài, ta có hệ phương trình sau:
a1 + a2 = 0.25(a1 + a2 + ... + ax) (1)
a1 + a2 + a3 = 0.6(a1 + a2 + ... + ax) (2)
Từ (1), ta có:
0.75(a1 + a2) = 0.75(a1 + a2 + ... + ax) (3)
Từ (2), ta có: 0.4(a1 + a2 + a3) = 0.4(a1 + a2 + ... + ax) (4)
Từ (3) và (4), ta có: 0.75(a1 + a2)
= 0.4(a1 + a2 + a3) 0.75a1 + 0.75a2
= 0.4a1 + 0.4a2 + 0.4a3 0.35a1 + 0.35a2
= 0.4a3
Từ đây, ta thấy rằng a1 + a2 phải lớn hơn a3.
Điều này chỉ xảy ra khi a1 + a2 + a3 là số lớn nhất trong tổng cân nặng của gia đình nhím.
Vậy, ta có thể kết luận rằng số thành viên trong gia đình nhím là 3.