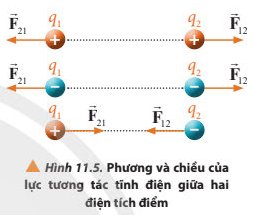
Các cặp lực \(\overrightarrow{F_{12}}\) và \(\overrightarrow{F_{21}}\) trong Hình 11.5 có phải là các cặp lực cân bằng không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi a, b, c là các đường thẳng lần lượt chứa các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \).
Khi đó: a, b, c lần lượt là giá của các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)
a) Dễ thấy: a // b // c
\( \Rightarrow \) Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) cùng phương với nhau.
Vậy các cặp vectơ cùng phương là: \(\overrightarrow a \) và \(\overrightarrow b \), \(\overrightarrow a \) và \(\overrightarrow c \), \(\overrightarrow b \) và \(\overrightarrow c \).
b) Quan sát ba vectơ, ta thấy: vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng xuống còn vectơ \(\overrightarrow b \) hướng lên trên.
Vậy vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng, vectơ \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng, vectơ \(\overrightarrow b \) và \(\overrightarrow c \) ngược hướng.

a)Gọi trọng lượng của ròng rọc 2 là \(P_1\)
Ở hình 1: \(F_1=\dfrac{P_A+P_1}{2}\Rightarrow P_1=2F_1-P_A\) (1)
Ở hình 2: \(F_2=\dfrac{\dfrac{P_B+P_1}{2}+P_1}{2}=\dfrac{P_B+3P_1}{4}\)
\(\Rightarrow P_1=\dfrac{4F_2-P_B}{3}\) (2)
Từ (1) và (2) \(\Rightarrow2F_1-P_A=\dfrac{4F_2-P_B}{3}\)
Mà \(P_A=P_B\); \(F_1=1000N;F_2=700N\)
\(\Rightarrow P_A=1600N\)
Lại có: \(P_A=10m_A\Rightarrow m_A=160kg\)\
b)Ròng rọc ở hệ thống 2.
Thấy 2 ròng rọc động\(\Rightarrow\) Lợi 4 lần về lực và thiệt 4 lần về đường đi.
\(\Rightarrow H=\dfrac{P_B\cdot h}{F_2\cdot S}=\dfrac{P_B\cdot h}{F_2\cdot4h}\cdot100\%\approx57\%\)

Chọn D
Cả ba cặp lực nói trên đều không phải là các cặp lực cân bằng vì:
Đáp án A: không phải lực cân bằng vì hai lực này cùng chiều.
Đáp án B: không phải lực cân bằng vì hai lực này đặt vào hai vật khác nhau.
Đáp án C: không phải lực cân bằng vì hai lực này cũng đặt vào hai vật khác nhau

Ta có: giá của \(\overrightarrow {AB} \) là đường thẳng AB, giá của \(\overrightarrow {CD} \)là đường thẳng CD, và thấy rằng 2 đường thẳng này trùng nhau suy ra giá của 2 vecto này trùng nhau.
Tương tự ta thấy giá của cặp \(\overrightarrow {PQ} \) và \(\overrightarrow {RS} \) song song với nhau.

Tham khảo:
Bước 1: Đặt \(\overrightarrow u = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \). Ta xác định các điểm như hình dưới.

Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto \(\overrightarrow u \) chính là vecto \(\overrightarrow {AC} \)
Vì chất điểm A ở trang thái cân bằng nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \) hay \(\;\overrightarrow u + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)
\( \Leftrightarrow \;\overrightarrow u \) và \(\;\overrightarrow {{F_3}} \) là hai vecto đối nhau.
\( \Leftrightarrow A\) là trung điểm của EC.
Bước 2:
Ta có: \(\left| {\overrightarrow {{F_1}} } \right| = AD = 20,\;\left| {\overrightarrow {{F_2}} } \right| = AB,\;\left| {\overrightarrow {{F_3}} } \right| = AC.\)
Do A, C, E thẳng hàng nên \(\widehat {CAB} = {180^o} - \widehat {EAB} = {60^o}\)
\(\begin{array}{l} \Rightarrow \widehat {CAD} = {90^o} - {60^o} = {30^o}\\ \Rightarrow \left\{ \begin{array}{l}AC = \frac{{AD}}{{\cos {{30}^o}}} = \frac{{40\sqrt 3 }}{3};\;\\AB = DC = AC.\sin {30^o} = \frac{{20\sqrt 3 }}{3}.\end{array} \right.\end{array}\)
Vậy \(\;\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3},\;\;\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}.\)

Lực mà lò xo tác dụng vào vật và lực mà vật tác dụng vào lò xo đặt vào hai vật khác nhau nên không cân bằng ⇒ Đáp án C.
Các cặp lực \(\overrightarrow {{F_{12}}} \) và \(\overrightarrow {{F_{21}}} \) có là những cặp lực cân bằng vì theo định luật III Newton ta có: Khi một vật tác dụng lực lên vật thể thứ hai, vật thứ hai sẽ tác dụng một lực cùng độ lớn và ngược chiều về phía vật thứ nhất.