Trong thí nghiệm Young về giao thoa ánh sáng, khoảng vân sẽ thay đổi thế nào khi ta thay nguồn sáng đơn sắc có bước sóng λ bằng ánh sáng đơn sắc có bước sóng là 1,2λ? Nếu khoảng cách từ hai khe đến màn quan sát giữ cố định, ta phải thay đổi khoảng cách giữa hai khe như thế nào để khoảng vẫn lại có độ lớn như ban đầu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Bước sóng của bức xạ cho vân sáng tại vị trí x: 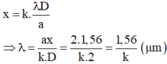
Cho λ vào điều kiện bước sóng ta có:
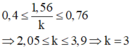
Bước sóng của ánh sáng dùng trong thí nghiệm là
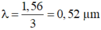

Cách giải: Đáp án D
Khoảng cách giữa hai vân sáng liền kề là một khoảng vân

Khoảng cách giữa 9 vân sáng liên tiếp là 25,3 mm :
\(8i=25,3\Leftrightarrow i=3,1625mm=3,1625.10^{-3}m\)
\(a=0,2mm=2.10^{-4}m\)
\(D=1m\)
\(a,\) Bước sóng : \(i=\dfrac{\lambda D}{a}\Leftrightarrow\lambda=\dfrac{ia}{D}=\dfrac{3,1625.10^{-3}.2.10^{-4}}{1}=6,325.10^{-7}\left(m\right)\)
\(b,\) Vân sáng bậc hai : \(x_{S2}=2i=2.3,1625.10^{-3}=6,325.10^{-3}\left(m\right)\)
Vân tối thứ tư : \(x_{T4}=\left(3+\dfrac{1}{2}\right)i=\dfrac{7}{2}.3,1625.10^{-3}=0,011\left(m\right)\)
Khoảng cách từ vân sáng bậc hai đến vẫn tối thứ tư ở cùng bên so với vân sáng trung tâm là :
\(d=\left|x_{T4}-x_{S2}\right|=\left|0,011-6,325.10^{-3}\right|=4,675.10^{-3}\left(m\right)\)
Vậy ...
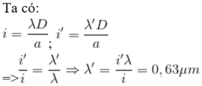


Ta có: \(i=\dfrac{\lambda D}{a}\)
Từ công thức ta thấy nếu λ tăng thành 1,2λ để giữ nguyên i thì phải tăng a thành 1,2a