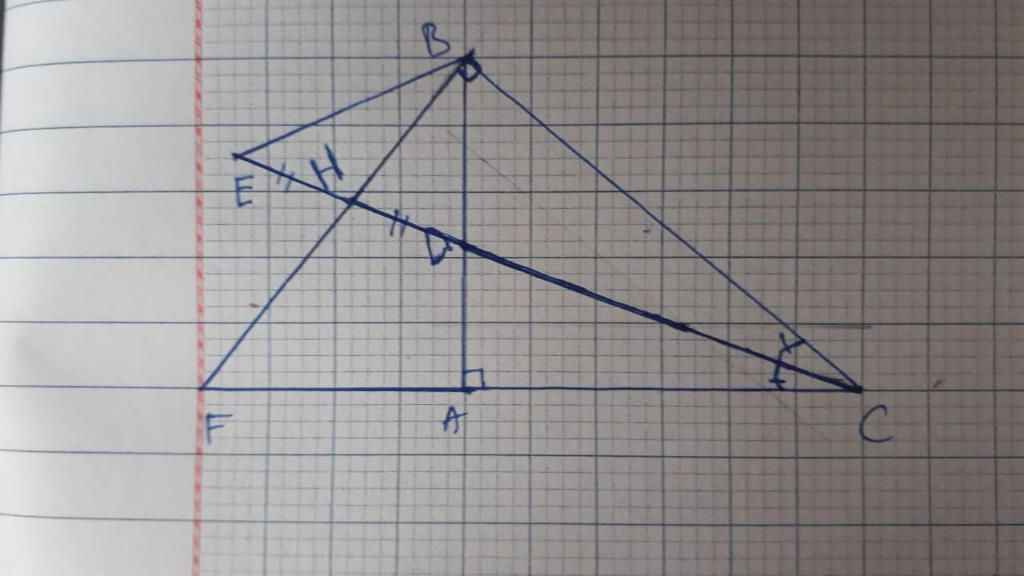
Cho tam giác ABC vuông ở A, phân giác CD. Gọi H là hình chiếu ủa B trên CD. Trên CD lấy E sao cho H là trung điểm cuả BE. Gọi F là giao điểm của BH và CA
chứng minh : a) \(\widehat{CEB}=\widehat{ADC}\) và \(\widehat{EBH}=\widehat{ACD}\)
b) B\(EB⊥BC\)
c) DF song song với BE