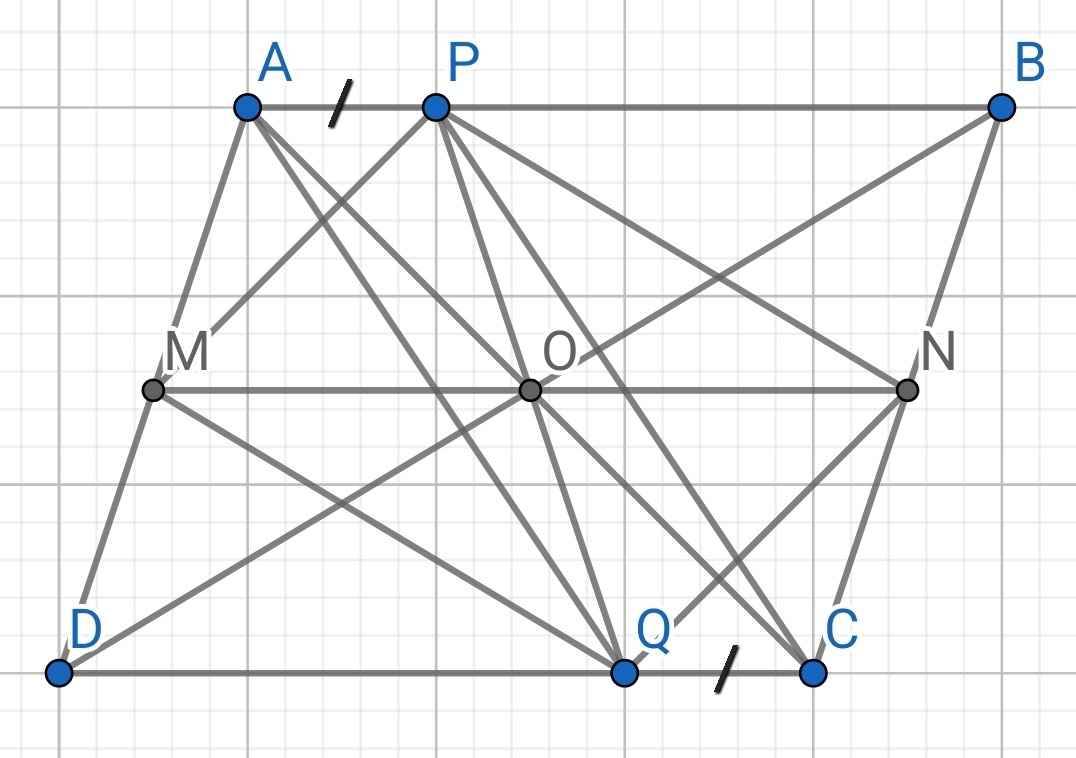
Cho hình bình hành ABCD. Gọi O là giao điểm hai đường thẳng AC và BD. Qua điểm O vẽ đường thẳng song song với AB cắt hai cạnh AD, BC lần lượt tại M,N. Trên AB, CD lần lượt lấy các điểm P, Q sap cho AP=CQ. Gọi I là giao điểm AC và PQ. Chứng minh:
a, Các tứ giác AMNB, APCQ là hình bình hành
b) Ba điểm M, N, I thẳng hàng
c)Ba đường thẳng AC, MN, PQ đồng quy
(mọi người có thể vẽ hình không cũng đc ạ, ko cần phải cminh ạ, mình cảm ơn)





a/
Ta có
MN//AB (gt)
AD//BC=> AM//BN
=> AMNB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có
AB//CD => AP//CQ mà AP = CQ (gt) => APCQ là hbh (Tứ giác có cặp cạnh đối // và = nhau là hbh)
b/
Xét hbh ABCD
OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Xét hbh APCQ có
IA=IC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> \(I\equiv O\) (đều là trung điểm AC) => M; N; I thẳng hàng
c/ Do \(I\equiv O\) (cmt) => AC; MN; PQ đồng quy tại O