So sánh pha dao động của thế năng và động năng khi vật dao động điều hòa.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Với hai dao động ngược pha, ta có: x 1 x 2 = A 1 A 2 = 2 → x 1 x 2 2 = E t 1 E t 2 = 4
Theo giả thuyết bài toán, ta có: E 1 − 0 , 48 0 , 04 = 4 E 1 − 0 , 04 E 2 t = 4 → E 2 t = 0 , 15 J

Ban đầu, động năng chiếm \(\delta\) phần, thế năng là 1 phần
Khi tốc độ giảm đi 1 nưa thì động năng còn \(\frac{\delta}{4}\), thế năng nhận thêm \(\frac{3\delta}{4}\), là \(1+\frac{3\delta}{4}=\frac{4+3\delta}{4}\)
Tỉ số động năng và thế năng lúc này: \(\frac{\frac{\delta}{4}}{\frac{4+3\delta}{4}}=\frac{\delta}{4+3\delta}\)
Chọn D.

Đáp án D
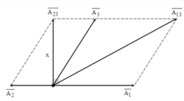
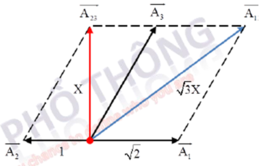
Biểu diễn vecto các dao động.
+ Ta có E 1 = 2 E 2 E 13 = 3 E 23 → A 1 = 2 A 2 A 13 = 3 A 23
Để đơn giản, ta chọn A 2 = 1 A 23 = x → A 1 = 2 A 13 = 3 x
+ Từ hình vẽ ta có 3 x 2 = x 2 + 1 + 2 2 → x = 1 + 2 2
Vì x 1 ⊥ x 23 nên biên độ của dao động tổng hợp của vật là A 2 = A 23 2 + A 1 2 = 1 + 2 2 2 + 2 2
→Ta có E E 23 = E W = A 2 A 23 2 = 1 + 2 2 2 + 2 2 1 + 2 2 2 ≈ 1 , 7

Đáp án D
Theo đề ta vẽ được giản đồ vecto như hình vẽ
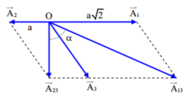
Ta có
![]()
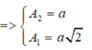
Từ hình vẽ ta có :
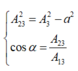
Theo đề
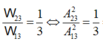
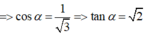
Lại có
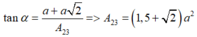
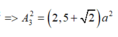
Vì
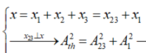
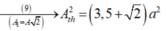
Ta có:
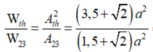
![]()
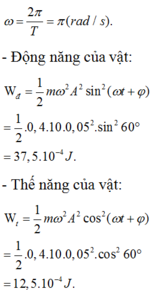



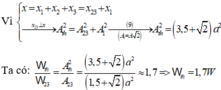

Tham khảo:
Trong quá trình vật dao động, khi động năng cực đại thì thế năng cực tiểu, khoảng thời gian ngắn nhất để chúng có cùng trạng thái là \(\Delta t=\dfrac{T}{4}\) nên độ lệch pha là\(\Delta\varphi=\dfrac{2\pi}{T}\cdot\dfrac{T}{4}=\dfrac{\pi}{2}\left(rad\right)\). Tức là động năng và thế năng vuông pha với nhau.