Bt:Mộtvậtnhỏđượcbắnlêntừmặtđấtvớigócbắn sovớiphươngngangvàvớivậntốcbanđầuvo =20m/s . Bỏ qua sức cản không khí và lấy g =10 m / s2 .
a) Tìm để vật có tầm xa bằng 30 m
b) Tìm để vật bay xa nhất và tính tầm xa cực đại đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2023
) Để tính tỉ số giữa độ cao cực đại và tầm xa của vật, ta cần tìm độ cao cực đại và tầm xa của vật. Độ cao cực đại (hmax) được tính bằng công thức: hmax = (v0^2 * sin^2(α)) / (2g) Tầm xa (R) được tính bằng công thức: R = (v0^2 * sin(2α)) / g Với α = 45°, ta có: hmax = (v0^2 * sin^2(45°)) / (2 * 10) = (v0^2 * 1/2) / 20 = v0^2 / 40 R = (v0^2 * sin(2 * 45°)) / 10 = (v0^2 * sin(90°)) / 10 = (v0^2 * 1) / 10 = v0^2 / 10 Tỉ số giữa độ cao cực đại và tầm xa của vật là: hmax / R = (v0^2 / 40) / (v0^2 / 10) = (10 * v0^2) / (40 * v0^2) = 1/4 Vậy tỉ số giữa độ cao cực đại và tầm xa của vật là 1/4. b) Để độ cao cực đại bằng với tầm xa của vật, ta cần giải phương trình: hmax = R (v0^2 / 40) = (v0^2 / 10) Với v0^2 khác 0, ta có: 1/40 = 1/10 Điều này là không thể xảy ra, vì vậy không tồn tại góc α để độ cao cực đại bằng với tầm xa của vật
VT
25 tháng 7 2018
Chọn đáp án C
Tầm bay xa của quả bóng là:
L = v0.t = 20.3 = 60 (m)
VT
7 tháng 11 2019
Đáp án C
Tầm bay xa của quả bóng là L = v 0 . t = 20.3 = 60 m
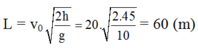
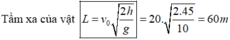
Ta có \(v_0=20\)(m/s)
Chiếu \(\overrightarrow{v_0}\) lên hệ trục Oxy
\(\Rightarrow v_x=v_0.\cos\alpha=20.\cos\alpha\) (m/s)
\(v_y=20.\sin\alpha\) (m/s)
Phương trình chuyển động
\(x=v_x.t=20\cos\alpha.t\)
\(y=v_y.t-\dfrac{1}{2}gt^2=20\sin\alpha.t-5t^2\)
mà \(x_{max}=30m\Leftrightarrow y=0\)
\(y=0\Leftrightarrow t=4\sin\alpha\)
Khi đó \(x_{max}=20\cos\alpha.t=30\left(m\right)\)
\(\Leftrightarrow\cos\alpha.\sin\alpha=\dfrac{3}{8}\)
\(\Leftrightarrow\sin\left(2\alpha\right)=\dfrac{3}{4}\)
\(\Leftrightarrow\alpha\approx24,3^{\text{o}}\)
b) Dựa vào câu a ta có vật đạt \(x_{max}\Leftrightarrow y=0\)
Khi đó ta có \(x_{max}=80.\sin\alpha.\cos\alpha=40.\sin2\alpha\)
mà \(\sin2\alpha\le1\) nên \(x_{max}\le80\) (m)
Dấu "=" khi \(\sin2\alpha=1\Leftrightarrow\alpha=45^{\text{o}}\)