Vận dụng được công thức \(E=\dfrac{\left|Q\right|}{4\pi\varepsilon_0r^2}\) để tính toán và mô tả điện trường của hệ nhiều điện tích, vật tích điện hình cầu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đoạn thẳng 1cm biểu diễn cho độ lớn của cường độ điện trường \(E = \frac{{{{10}^{ - 10}}}}{{6\pi {\varepsilon _0}}} = 0,6\)V/m.
Cường độ điện trường tại điểm cách Q một khoảng 2 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{02}^2}}} = 1,34\)V/m
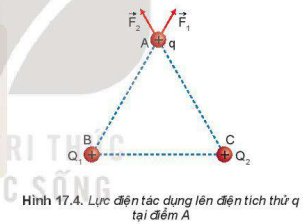
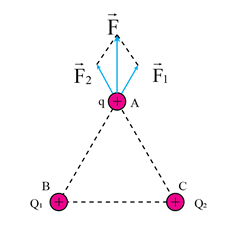
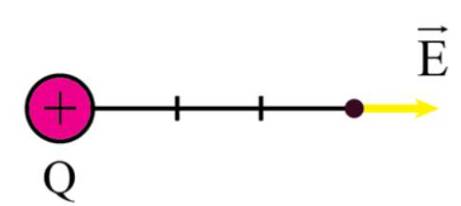
Vectơ cường độ điện trường:
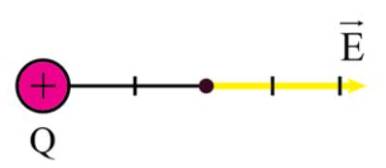
Cường độ điện trường tại điểm cách Q một khoảng 3 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{03}^2}}} = 0,6\)V/m
Vectơ cường độ điện trường:

Công thức 19.2:
\(W_M=A_{M\infty}\)
Công thức 19.3:
\(W_M=V_Mq\)
Điện thế tại điểm M:
\(V_M=\dfrac{W_M}{q}=\dfrac{A_{M\infty}}{q}\) và \(V=\dfrac{A}{q}\)

Lực điện tác dụng lên quả cầu là: \(F=E\left|q\right|=10^3.10^{-6}=10^{-3}N\)
mà F=ma \(\Rightarrow a=\dfrac{F}{m}=\dfrac{10^{-3}}{5.10^{-3}}=0,2\)m/s2
Có: \(MN=\dfrac{1}{2}at^2=\dfrac{1}{2}.0,2.2^2=0,4m\)
Hiệu điện thế giữa hai điểm MN là: \(V_{MN}=E.MD=10^3.0,4=400V\)

Độ lớn cường độ điện trường tại 1 điểm:
\(E=k\dfrac{\left|Q\right|}{r^2}\)
Lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó:
\(E=\dfrac{F}{q}=\dfrac{k\dfrac{\left|Q\cdot q\right|}{r^2}}{q}=k\dfrac{\left|Q\right|}{r^2}\)
Chứng tỏ: Độ lớn cường độ điện trường tại một điểm bằng độ lớn của lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó.