Ta có thể sử dụng định luật bảo toàn cơ năng để tìm li độ và vận tốc của vật dao động điều hòa được không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
6 tháng 1 2018
1. Goi A là đỉnh dốc, B là chân dốc
Chọn mốc thế năng nằm tại chân dốc
a. Theo định luật bảo toàn cơ năng
W A = W B ⇒ m g z A = 1 2 m v B 2 ⇒ v B = 2 g z A = 2.10.0.45 = 3 ( m / s )
b. Gọi C là vị trí W d = 2 W t . Theo định luật bảo toàn cơ năng
W A = W C ⇒ m g z A = W d C + W t C = 3 W t C = 3 m g z C ⇒ z C = z A 3 = 0 , 45 3 = 0 , 15 ( m )
Theo bài ra
W d = 2 W t ⇒ 1 2 m v C 2 = 2 m g z C ⇒ v C = 4. g z C = 4.10.0 , 15 = 6 ( m / s )
Thế năng của vật tại C
W t C = m g z C = 0 , 9.10.0 , 15 = 1 , 35 ( J )
2. a. Quãng dường chuyển động của vật
s = 75 − 27 = 48 ( c m ) = 0 , 48 ( m )
Theo định lý động năng ta có
A = W d 2 − W d 1 ⇒ P x . s = 1 2 m v 2 2 ⇒ m g . sin α = 1 2 m v 2 2 ⇒ v 2 = 2 g . sin α . s
Mà sin α = 45 75 => v 2 = 2.10. 45 75 .0 , 48 = 2 , 4 ( m / s )
b. Theo định lý động năng
A / = W d 3 − W d 1 ⇒ P x s / = 1 2 m v 3 2 ⇒ P sin α . s / = 1 2 m v 3 2 ⇒ g . sin α . s / = 1 2 v 3 2 ⇒ s / = v 3 2 2. g . sin α = 1 , 2 2.10. 45 75 = 0 , 1 ( m )
Vậy vật đi được quãng đường 10cm
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
Vì vận tốc tức thời được tính bằng công thức:
\(v=\dfrac{\Delta x}{\Delta t}\)
Và gia tốc tính bằng công thức:
\(a=\dfrac{\Delta x}{\Delta v}\)
H
1 tháng 3 2021
Bài 1 :
Chọn mốc thế năng tại mặt đất.
\(W = \dfrac{1}{2}mv^2 + mgz = \dfrac{1}{2}.1.5^2 + 1.10.45=462,5(J)\)
H
1 tháng 3 2021
Bài 2 :
Chọn mốc thế năng tại mặt đất.
a)
Cơ năng tại A :
\(W_A = W_{đ_A} + W_{t_A}\)
Tại độ cao 25m :
\(W = W_{đ} +W_t\)
Bảo toàn cơ năng :\(W_A =W\)
Suy ra:
\(W_đ+W_t = W_{t_A}\\ \Leftrightarrow W_đ = 0,5.10.80 - 0,5.10.25 = 275(J)\)
b)
\(s = v_ot + \dfrac{1}{2}gt^2 = 0,5.10.t^2 = 25\Rightarrow t = \sqrt{5}\\ \Rightarrow v = gt = 10\sqrt{5}\)
Ta có :
\(W = \dfrac{1}{2}mv^2 = 0,5.2.(10\sqrt{5})^2 = 500(J)\)
24 tháng 2 2021
a) Độ cao vật đi thêm được:
v2 - v02 = 2as = -2ghmax ⇒ hmax = \(\dfrac{-10}{-2.10}=0,5m\)
Độ cao cực đại của vật:
s = h + hmax = 5 + 0,5 = 5,5m
b) Vận tốc của vậy lúc chạm đất:
Wtmax = Wdmax ⇒ mgs = \(\dfrac{1}{2}.m.v^2_{max}\Rightarrow v_{max}=\sqrt{2.g.s}=\sqrt{2.10.5,5}=\sqrt{110}m/s\)
c) Áp dụng định luật bảo toàn cơ năng:
W = Wdat <=> mgh + \(\dfrac{1}{2}mv^2_0=\dfrac{1}{2}mv^2\)
\(\Leftrightarrow gh+\dfrac{1}{2}v^2_0=\dfrac{1}{2}v^2\)
\(\Leftrightarrow10.5+\dfrac{1}{2}.10=\dfrac{1}{2}v^2\)
\(\Leftrightarrow v=7,5m/s\)
HQ
25 tháng 2 2021
\(h_{max}=\dfrac{-v_0^2}{-2g}\) ( quên bình ở vận tốc kìa bạn :v )
MN
10 tháng 6 2021
Cơ năng của vật ở độ cao 40 m là :
\(W^`=W_t^`=m\cdot g\cdot z=1\cdot40\cdot10=400\left(J\right)\)
Định luật bảo toàn cơ năng :
\(W=W^`=400\left(J\right)\)
\(\Leftrightarrow\dfrac{1}{2}\cdot m\cdot v^2=400\)
\(\Leftrightarrow v=20\sqrt{2}\left(\dfrac{m}{s}\right)\)
HD
Hà Đức Thọ
Admin
27 tháng 5 2015
Câu này sai luôn ở ý A, khi qua VTCB thì lực gây nên dao động của vật bằng 0.
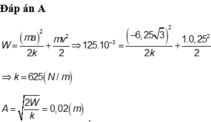
Với định luật bảo toàn cơ năng ta có thể tìm được li độ và vận tốc vật trong dao động điều hòa:
\(W_đ=W_t=W\)
\(\Leftrightarrow\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2x^2=\dfrac{1}{2}m\omega^2A^2\)