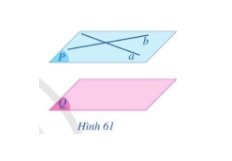
Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
Nếu hai mặt phẳng (P) và (Q) có một điểm chung thì chúng có đường thẳng chung d.
Ta có: a // (Q);
a ⊂ (P);
(P) ∩ (Q) = d.
Suy ra a // d.
Tương tự ta cũng có b // d.
Mà a, b, d cùng nằm trong mặt phẳng (P) nên a // b // d, điều này mâu thuẫn với giả thiết a, b cắt nhau trong (P).
Vậy hai mặt phẳng (P) và (Q) không có điểm chung hay (P) // (Q).
CM
5 tháng 2 2018
Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
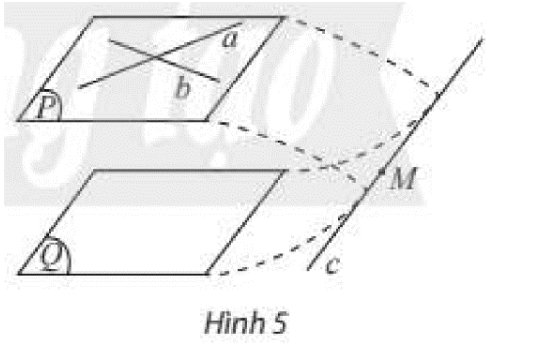
a) Gọi \(I\) là giao điểm của \(a\) và \(b\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}a\parallel \left( Q \right)\\\left( P \right) \supset a\\\left( P \right) \cap \left( Q \right) = c\end{array} \right\} \Rightarrow c\parallel a\\\left. \begin{array}{l}b\parallel \left( Q \right)\\\left( P \right) \supset b\\\left( P \right) \cap \left( Q \right) = c\end{array} \right\} \Rightarrow c\parallel b\end{array}\)
Do đó qua \(I\) ta kẻ được hai đường thẳng \(a\) và \(b\) cùng song song với \(c\), mâu thuẫn với định lí qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
Vậy \(c\) phải cắt ít nhất một trong hai đường thẳng \(a,b\).
Nếu đường thẳng \(c\) cắt đường thẳng \(a\) hoặc đường thẳng \(b\), mà đường thẳng \(c\) nằm trong mặt phẳng \(\left( Q \right)\), khi đó đường thẳng \(a\) hoặc đường thẳng \(b\) có 1 điểm chung với mặt phẳng \(\left( Q \right)\). Điều này trái với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\).
b) Vì \(\left( P \right)\) chứa đường thẳng \(a\) mà \(a\) song song với mặt phẳng \(\left( Q \right)\) nên \(\left( P \right)\) và \(\left( Q \right)\) là hai mặt phẳng phân biệt.
Theo chứng minh ở trên, nếu \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung \(M\) thì mâu thuẫn với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\).
Vậy hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) không có điểm chung.
14 tháng 7 2023
bạn Minh phát biểu sai vì \(\dfrac{CA}{C'A'}=\dfrac{AB+BC}{A'B'+C'B'}\ne\dfrac{AB}{BC}\ne\dfrac{A'B'}{C'B'}\)
CM
21 tháng 1 2019
Đáp án B.
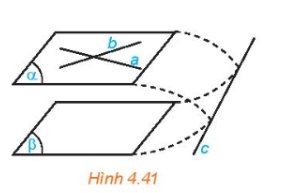
Theo định lý, nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau và cùng song song với mặt phẳng (Q) thì (P) song song với (Q), do đó nếu lấy mọi đường thẳng nằm trong mặt phẳng (P) thì tồn tại hai đường thẳng cắt nhau thỏa mãn định lý, vậy phát biểu (2) đúng.
Phát biểu (1) sai vì hai đường thẳng đó có thể chéo nhau.
Chọn đáp án B
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
Trường hợp a cắt b theo dấu hiệu nhận biết hai mặt phẳng song song thì ý kiến đúng
Trường hợp a không cắt b thì a//b
Ta có: a thuộc (P), a//(Q)
B thuộc (P), b//(Q)
Do đó: (P)//(Q)
=>Ý kiến này đúng trong cả hai trường hợp