giúp tớ với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: \(n_{CH_3COOH}=\dfrac{60}{60}=1\left(mol\right)\)
a, PT: \(2CH_3COOH+K_2CO_3\rightarrow2CH_3COOK+CO_2+H_2O\)
_________1____________________1_________0,5 (mol)
b, VCO2 = 0,5.22,4 = 11,2 (l)
c, mCH3COOK = 1.98 = 98 (g)
Bạn tham khảo nhé!
a) PTHH: 2CH3COOH + K2CO3 → 2CH3COOK + CO2↑ + H2O
b) nCH3COOH = \(\dfrac{m}{M}=\dfrac{60}{60}=1\left(mol\right)\)
Theo PTHH: nCO2 = \(\dfrac{1}{2}\).nCH3COOH = 0,5 (mol)
=> VCO2 (đktc) = n.22,4 = 0,5.22,4 = 11,2 (lít)
c) Theo PTHH: nCH3COOK = nCH3COOH = 1 (mol)
=> mCH3COOK = n.M = 1.98 = 98 (g)
Mặc dù hơi muộn nhưng mà chúc bạn thi đạt kết quả tốt nha ^_^




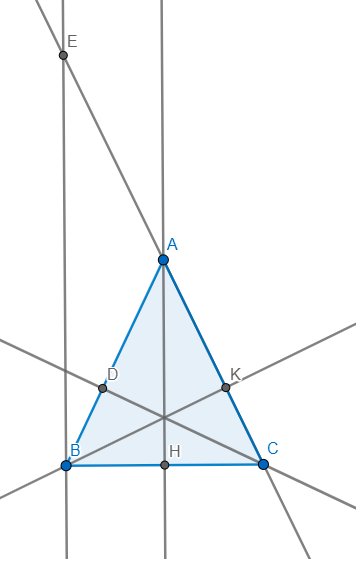
b) Từ B kẻ đường vuông góc với BC cắt AC tại E
tam giác BEC vuông tại B có \(AB=AC\Rightarrow A\) là trung điểm CE
Vì tam giác ABC cân tại A có AH là đường cao \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow AH\) là đường trung bình tam giác BEC
\(\Rightarrow AH=\dfrac{1}{2}BE\Rightarrow2AH=BE\Rightarrow4AH^2=BE^2\)
tam giác BEC vuông tại B có BK là đường cao \(\Rightarrow\dfrac{1}{BE^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
\(\Rightarrow\dfrac{1}{4AH^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)






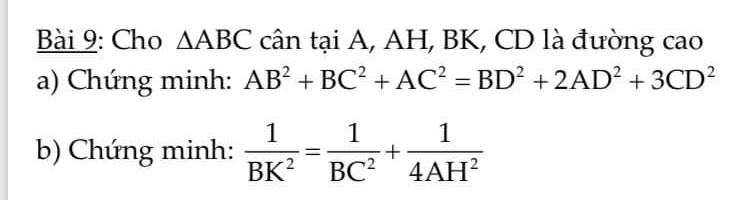



Tg ABC cân
=> AB=AC (1)
AN=BN (gt) (2); AM=CM (gt) (3)
Xét tg ABM và tg ACN có
\(\widehat{A}\) chung
AB=AC
Từ (1) (2) (3)
\(\Rightarrow AN=AM\)
=> tg ABM = tg ACN (c.g.c) => BM=CN
b/
Ta có G là trong tâm của tg ABC
\(\Rightarrow GM=\dfrac{1}{3}BM\Rightarrow GM=\dfrac{1}{2}BG\Rightarrow BG=2.GM\)
\(\Rightarrow GN=\dfrac{1}{3}CN\Rightarrow GN=\dfrac{1}{2}CG\)
Mà BM=CN (cmt) => GM=GN => BG = CG = 2.GM
Xét tg BGC có
\(BC< BG+CG\) (trong tg dộ dài 1 cạnh nhỏ hơn tổng độ dài 2 cạnh còn lại)
\(\Rightarrow BG+CG>BC\Rightarrow4.GM>BC\Rightarrow GM>\dfrac{1}{4}BC\)