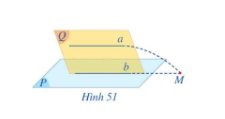
Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyển b. (Hình 51)a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì...
Đọc tiếp
Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyển b. (Hình 51)
a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?
b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?
a) Ta có a ∩ b = {M} nên M ∈ b
Mà b ⊂ (P), do đó M ∈ (P).
Lại có M ∈ a.
Vậy đường thẳng a cắt mặt phẳng (P) tại M.
b) Theo câu a, nếu a cắt b tại M thì a cắt (P) tại M, điều này mâu thuẫn với giả thiết đường thẳng a song song với mặt phẳng (P).
Do đó a và b không cắt nhau và cùng nằm trong mặt phẳng (Q).
Suy ra a // b.
Vậy hai đường thẳng a và b song song với nhau.