Từ một điểm A\(\in\)(O;R) vẽ tiếp tuyến Ax. Lấy I \(\in\)Ax sao cho \(AI=R\sqrt{3}\). Lấy B \(\in\)(O) sao IB = IA
a. Tính \(\widehat{AIO}\)
b. Tính \(\widehat{AIB}\)
c. Kéo dài BO cắt tia IA = k. Tính các cạnh tam giác IBK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2023
a: ΔOAB cân tại O
mà OH là trung tuyến
nên OH vuông góc AB
góc OHI=góc OMI=góc ONI=90 độ
=>O,H,M,I,N cùng thuộc đường tròn đường kính OI
=>ĐPCM
b: Xét (O) co
IM,IN là trung tuyến
=>IM=IN
mà OM=ON
nên OI là trung trực của MN
=>OI vuông góc MN tại J
Xet ΔIJK và ΔIHO có
góc IJK=góc IHO
góc JIK chung
=>ΔIJK đồng dạng với ΔIHO
=>IJ/IH=IK/IO
=>IK*IH=IJ*IO
c: sin MIO=OM/OI=1/2
=>góc MIO=30 độ
=>góc MIN=60 độ
\(IM=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
\(S_{IMN}=\left(R\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{3\cdot R^2\cdot\sqrt{3}}{4}\)
14 tháng 1 2023
6.1:
Xét (O) có
MA,MB là tiếp tuyến
nên MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc với AB
Xét ΔOAM vuông tại A có AH là đường cao
nên OH*OM=OA^2
=>OH*8=4^2=16
=>OH=2cm
Xét ΔAMO vuông tại A có sin AMO=AO/OM=1/2
nên góc AMO=30 độ
6.2:
Xét ΔMAB có MA=MB và góc AMB=60 độ
nên ΔMAB đều
6.3:
Xét tứ giác AHIM có
góc AHM=góc AIM=90 độ
nên AHIM là tứ giác nội tiếp
CM
12 tháng 8 2019
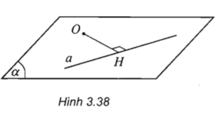
Khoảng cách từ điểm O đến đường thẳng a là OH (H là hình chiếu vuông góc của O trên a)
Dựa vào quan hệ giữa đường xiên và đường vuông góc ⇒ khoảng cách từ điểm O đến đường thẳng a là bé nhất so với các khoảng cách từ O đến một điểm bất kì của đường thẳng a
17 tháng 12 2021
Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
A I B O K C
\(\Delta AIO;BIO\)Có \(\hept{\begin{cases}0A=0B=R\\IA=IB=\sqrt{3}R\\OI\left(chung\right)\end{cases}}\)\(\Rightarrow\widehat{IAO}=\widehat{IBO}=90^0\)
\(Sin\widehat{KIB}=\frac{BK}{IK}\Rightarrow IK=\frac{BK}{Sin\widehat{KIB}}=\frac{3R}{Sin60^0}\frac{3R}{\frac{\sqrt{3}}{2}}=2\sqrt{3}.R\)