Question

[Đào Hương Nguyên]

giúp mình với nhanh nhanh nha mình đag cần gấp á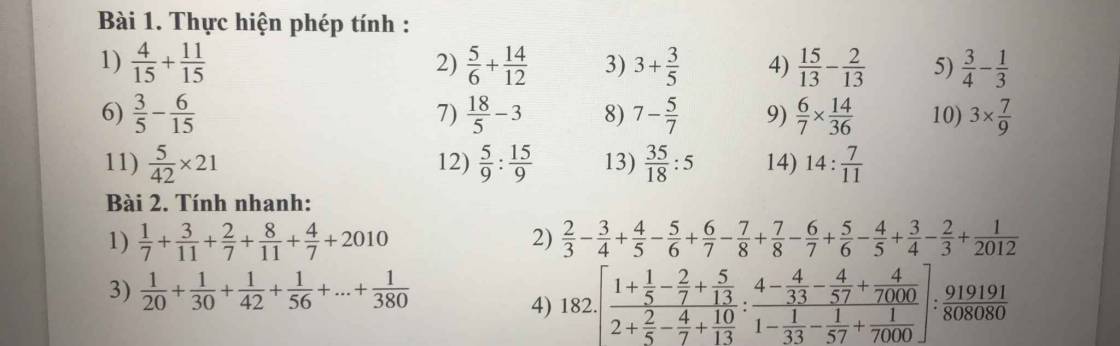

Answer 1

[Akai Haruma]

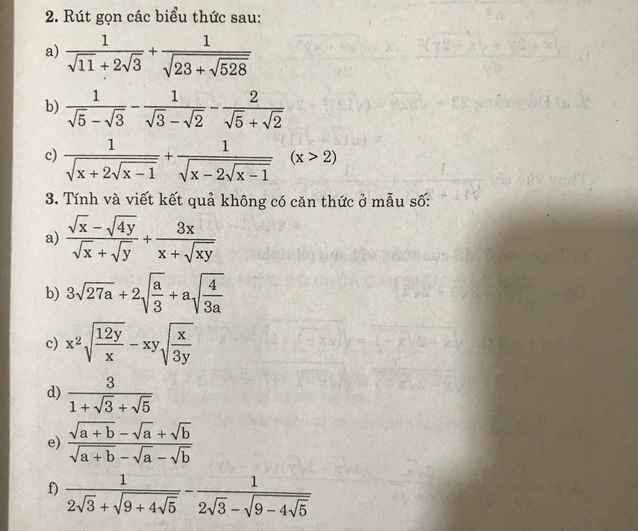
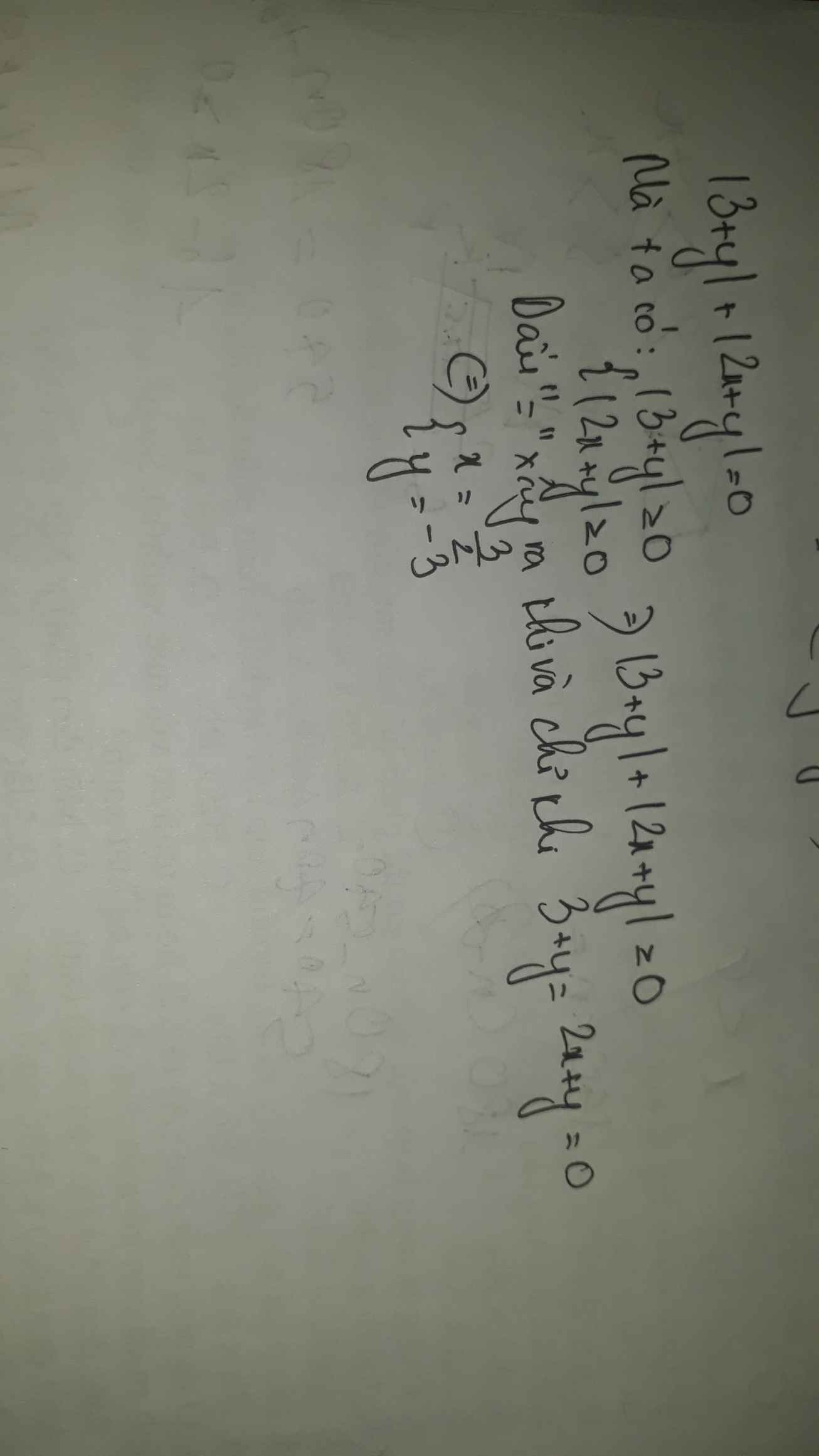
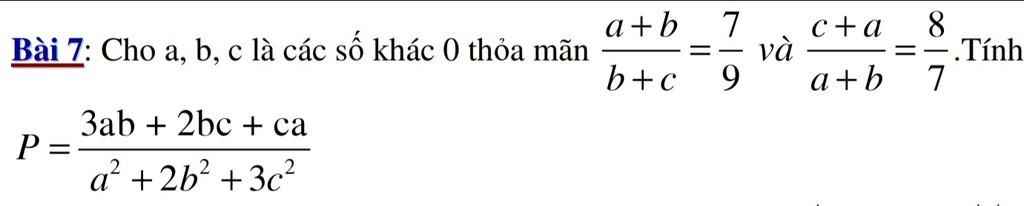
Bài 2:

1.

$=(\frac{1}{7}+\frac{2}{7}+\frac{4}{7})+(\frac{3}{11}+\frac{8}{11})+2010$

$=\frac{7}{7}+\frac{11}{11}+2010=1+1+2010=2012$
2.

$=(\frac{2}{3}-\frac{2}{3})+(\frac{-3}{4}+\frac{3}{4})+(\frac{4}{5}-\frac{4}{5})+(\frac{-5}{6}+\frac{5}{6})+(\frac{6}{7}-\frac{6}{7})+(\frac{-7}{8}+\frac{7}{8})+\frac{1}{2012}$

$=0+0+0+0+0+0+\frac{1}{2012}=\frac{1}{2012}$

3.

$=\frac{1}{5-4}{4.5}+\frac{6-5}{5.6}+\frac{7-6}{6.7}+...+\frac{1}{20-19}{19.20}$

$=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+..+\frac{1}{19}-\frac{1}{20}$

$=\frac{1}{4}-\frac{1}{20}=\frac{1}{5}$

4.

\(=182\left[\frac{1+\frac{1}{5}-\frac{2}{7}+\frac{5}{13}}{2(1+\frac{1}{5}-\frac{2}{7}+\frac{5}{13})}: \frac{4(1-\frac{1}{33}-\frac{1}{57}+\frac{1}{7000})}{1-\frac{1}{33}-\frac{1}{57}+\frac{1}{7000}}\right]:\frac{10101\times 91}{10101\times 80}\)

$=182(\frac{1}{2}:4):\frac{91}{80}=182\times \frac{1}{8}\times \frac{80}{91}$

$=\frac{91\times 2\times 80}{8\times 91}=\frac{160}{8}=20$