Cho tam giác ABC. Trên cạnh AB lấy điểm K. Kẻ KH//BC ( H ϵ AC ). Gọi E là giao điểm của BH với KC. Tia AE cắt KH và BC lần lượt tại I và Q. Chứng minh rằng:
a, IK/QB = IH/QC
b, IK/QC = IH/QB
c, QB = QC
d, IK = IH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAIB và ΔAIC có
AB=AC
\(\widehat{BAI}=\widehat{CAI}\)
AI chung
Do đó: ΔAIB=ΔAIC
b: ΔAIB=ΔAIC
=>IB=IC và \(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC
b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
\(\widehat{HAI}=\widehat{KAI}\)
Do đó: ΔAHI=ΔAKI
=>IH=IK
c: Xét ΔHIN vuông tại H và ΔKIM vuông tại K có
IH=IK
\(\widehat{HIN}=\widehat{KIM}\)
Do đó: ΔHIN=ΔKIM
=>IN=IM và HN=KM
ΔAHI=ΔAKI
=>AH=AK
AH+HN=AN
AK+KM=AM
mà AH=AK và HN=KM
nên AN=AM
=>A nằm trên đường trung trực của NM(1)
IN=IM(cmt)
nên I nằm trên đường trung trực của MN(2)
PN=PM
=>P nằm trên đường trung trực của MN(3)
Từ (1),(2),(3) suy ra A,I,P thẳng hàng

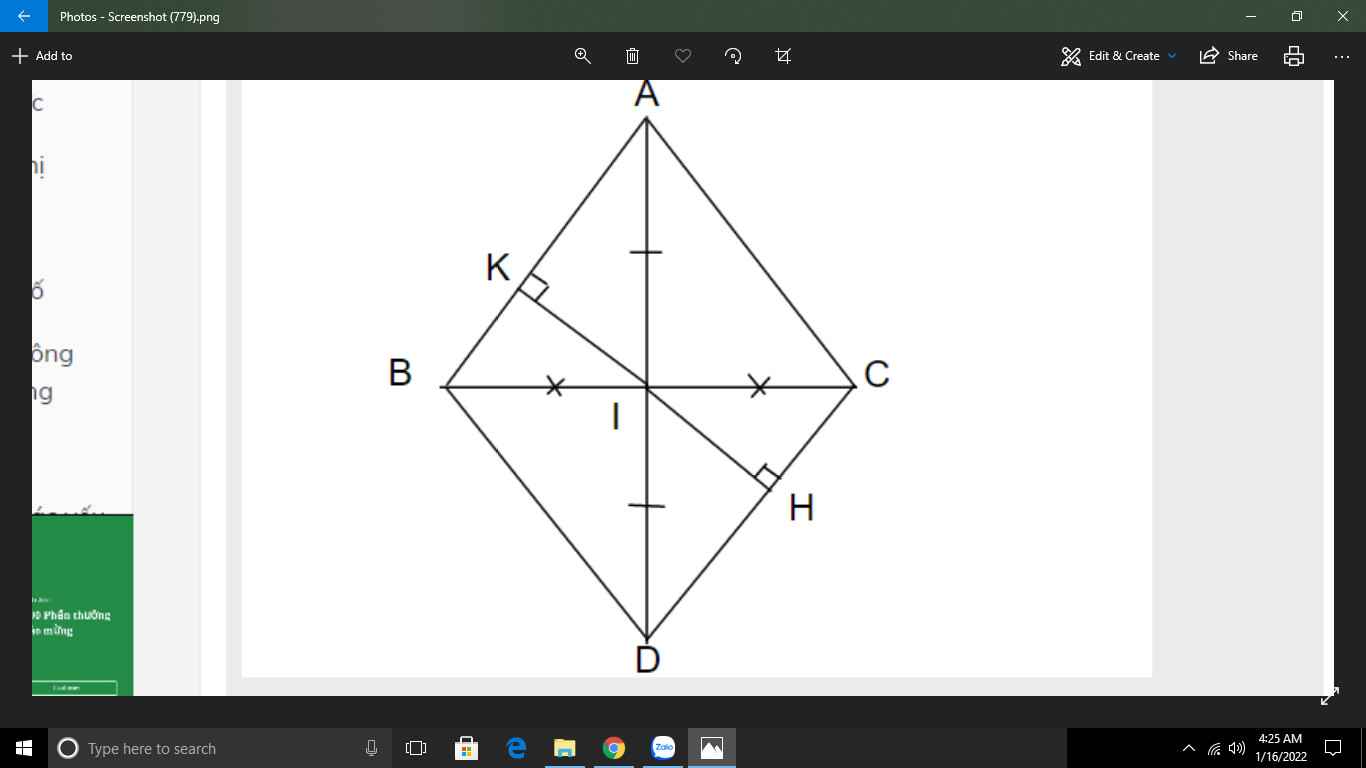
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)

b: Xét ΔABC có
I là trung điểm của BC
IH//AC
Do đó: H là trung điểm của AB
Xét tứ giác AIBQ có
H là trung điểm của đường chéo AB
H là trung điểm của đường chéo IQ
Do đó: AIBQ là hình bình hành
mà AB\(\perp\)IQ
nên AIBQ là hình thoi
a: Xét ΔABQ có IK//BQ
nen IK/QB=AI/AQ
Xét ΔAQC có IH//QC
nên IH/QC=AI/AQ
=>IK/QB=IH/QC
b,c,d: Cái đề này phải bổ sung thêm là Q là trung điểm của BC á nha bạn
a,Xét tam giác ABQ có IK//BQ ( vì KH// BC)
=> `(IK)/(QB) = (AI)/(AQ)` (1)
Xét tam giác ACQ có IH//QC ( vì KH// BC)
=>`(IH)/(QC) = (AI)/(AQ)` (2)
Từ (1) và (2) => `(IK)/(QB) = (IH)/(QC)`
b,Xét tam giác EQC có IK//QC ( vì KH// BC)
=> `(IK)/(QC) = (IE)/(EQ)` (3)
CMTT => `(IH)/(BQ) = (IE)/(EQ)` (4)
Từ (3) và (4) => `(IH)/(BQ) = (IK)/(QC)`
c,Từ `(IK)/(QB) = (IH)/(QC)` và `(IH)/(BQ) = (IK)/(QC)`
=> `(IK)/(QB)` . `(IH)/(QB)` = `(IH)/(QC)` . `(IK)/(QC)`
=> `(IK . IH)/(QB . QB)` = `(IH . IK)/(QC .QC)`
=> `QB^2 = QC^2` => QB=QC
d, Từ QB=QC và `(IK)/(QB) = (IH)/(QC)` => IK=IH