giúp e bài 1 vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 2 2022
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
22 tháng 7 2023
a: Xét ΔABC vuông tại A có sin C=AB/BC
=>6/BC=sin30=1/2
=>BC=12cm
=>AC=6*căn 3(cm)
HB=AB^2/BC=3cm
HC=12-3=9cm
b: Xét ΔABH vuông tại H có sin B=AH/AB=1/2
=>góc B=30 độ
=>góc C=60 độ
BH=căn 12^2-6^2=6*căn 3(cm)
CH=AH^2/HB=2*căn 3(cm)
AH
Akai Haruma
Giáo viên
14 tháng 8 2023
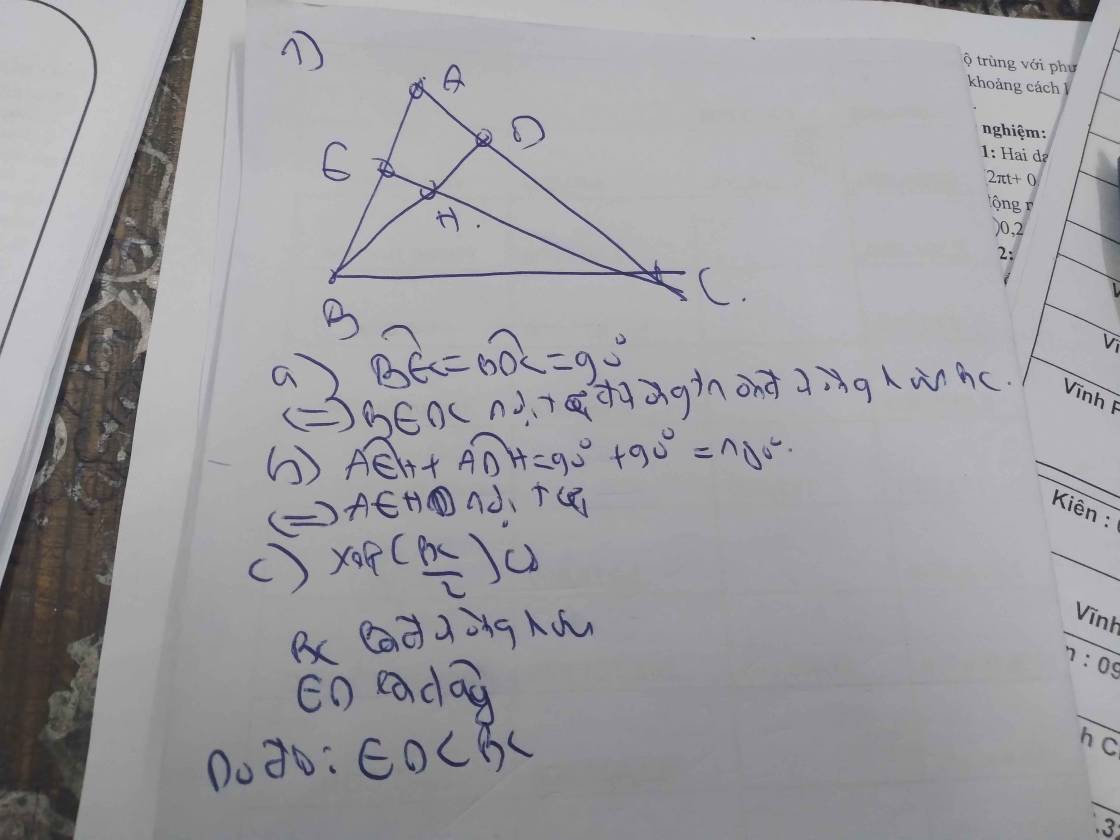
Bài 1:
a. Vì $BD, CE$ là đường cao nên $\widehat{BEC}=\widehat{BDC}=90^0$
Mà 2 góc này cùng nhìn cạnh $BC$ nên $BEDC$ là tứ giác nội tiếp.
Hay $B,E,D,C$ cùng thuộc 1 đường tròn.
b. Xét tứ giác $AEHD$ có tổng 2 góc đối nhau $\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0$ nên $AEHD$ là tứ giác nội tiếp
Hay $A,E,H,D$ cùng thuộc 1 đường tròn.
c.
Gọi $I$ là trung điểm $BC$
Xét tam giác $BEC$ vuông tại $E$ nên đường trung tuyến $EI= \frac{BC}{2}=IB=IC$
Tương tự: $DI=IB=IC$
Do đó: $IE=ID=IB=IC$ nên $I$ là tâm đường tròn ngoại tiếp tứ giác $BEDC$
$\Rightarrow BC$ là đường kính
$\Rightarrow BC> ED$
MN
26 tháng 8 2021
Bảo toàn nguyên tố O :
\(n_{H_2O\left(TN1\right)}=n_{H_2O\left(TN2\right)}=0.08\left(mol\right)\)
Ở TN2, Bảo toàn nguyên tố H :
\(n_H=2\cdot n_{H_2O}=2\cdot0.08=0.16\left(mol\right)\)
Với cùng nồng độ mol thì : tỉ lệ số mol giữa HCl và H2SO4 : \(\dfrac{1}{0.5}=\dfrac{2}{1}\)
\(n_{HCl}=2a\left(mol\right),n_{H_2SO_4}=a\left(mol\right)\)
\(\Rightarrow n_H=2a+a\cdot2=0.16\left(mol\right)\)
\(\Rightarrow a=0.04\)
\(m_{Muối}=m_X+m_{HCl}+m_{H_2SO_4}-m_{H_2O}=5+0.08\cdot36.5+0.04\cdot98-0.08\cdot18=10.4\left(g\right)\)
\(1.\)
\(a,\)
\(3x^2-6xy+3y^2\)
\(=3\left(x^2-2xy+y^2\right)\)
\(=3\left(x-y\right)^2\)
\(b,\)
\(12x^5y+24x^4y^2+12x^3y^3\)
\(=12x^3y\left(x^2+2xy+y^2\right)\)
\(=12x^3y\left(x+y\right)^2\)
\(c,\)
\(64xy-96x^2y+48x^3y-8x^4y\)
\(=8xy\left(8-12x+6x^2-x^3\right)\)
\(=8xy\left(2-x\right)^3\)
\(d,\)
\(54x^3+16y^3\)
\(=2\left(27x^3+8y^3\right)\)
\(=2\left[\left(3x\right)^3+\left(2y\right)^3\right]\)
\(=2\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)\)
\(2.\)
\(a,\)
\(x^2-2xy+y^2-4\)
\(=\left(x^2-2xy+y^2\right)-4\)
\(=\left(x-y\right)^2-2^2\)
\(=\left(x-y-2\right)\left(x-y+2\right)\)
\(b,\)
\(-16x^2+8xy-y^2+49\)
\(=49-\left(16x^2-8xy+y^2\right)\)
\(=7^2-\left(4x-y\right)^2\)
\(=\left(7-4x+y\right)\left(7+4x-y\right)\)
\(3.\)
\(a,\)
\(x^6-x^4+2x^3+2x^2\)
\(=x^2\left(x^4-x^2+2x+2\right)\)
\(=x^2\left[x^2\left(x^2-1\right)+2\left(x+1\right)\right]\)
\(=x^2\left[x^2\left(x-1\right)\left(x+1\right)+2\left(x+1\right)\right]\)
\(=x^2\left(x+1\right)\left[x^2\left(x-1\right)+2\right]\)
\(=x^2\left(x+1\right)\left(x^3-x^2+2\right)\)
\(=x^2\left(x+1\right)\left(x^3+x^2-2x^2-2x+2x+2\right)\)
\(=x^2\left(x+1\right)\left[x^2\left(x+1\right)-2x\left(x+1\right)+2\left(x+1\right)\right]\)
\(=x^2\left(x+1\right)\left(x+1\right)\left(x^2-2x+2\right)\)
\(=x^2\left(x+1\right)^2\left(x^2-2x+2\right)\)
\(b,\)
\(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=\left(x+y-x+y\right)\left[\left(x+y\right)^2+\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\right]\)
\(=2y\left(x^2+2xy+y^2+x^2-y^2+x^2-2xy+y^2\right)\)
\(=2y\left(3x^2+y^2\right)\)
1:
a: =3(x^2-2xy+y^2)
=3(x-y)^2
b: \(=12x^3y\left(x^2+2xy+y^2\right)=12x^3y\left(x+y\right)^2\)
c: \(=8xy\left(8-12x+6x^2-x^3\right)\)
=8xy(2-x)^3
d: =2(27x^3+8y^3)
=2(3x+2y)(9x^2-6xy+4y^2)