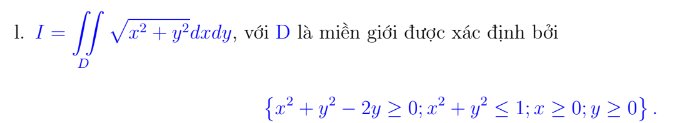
Tính tích giúp e với ạ .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2023
a, \(n_{Zn}=\dfrac{19,5}{65}=0,3\left(mol\right)\)
PT: \(Zn+2HCl\rightarrow ZnCl_2+H_2\)
Theo PT: \(n_{H_2}=n_{Zn}=0,3\left(mol\right)\Rightarrow V_{H_2}=0,3.22,4=6,72\left(l\right)\)
b, \(n_{CuO}=\dfrac{30}{80}=0,375\left(mol\right)\)
PT: \(CuO+H_2\underrightarrow{t^o}Cu+H_2O\)
Xét tỉ lệ: \(\dfrac{0,375}{1}>\dfrac{0,3}{1}\), ta được CuO dư.
Theo PT: \(n_{Cu}=n_{H_2}=0,3\left(mol\right)\Rightarrow m_{Cu}=0,3.64=19,2\left(g\right)\)
17 tháng 12 2021
Diện tích là:
\(\left(34.5:2\right)^2=297.5625\left(m^2\right)\)
DT
18 tháng 1 2022
Áp dụng đ/l pytago vào Δ vuông ABC tại B ta có :
\(AC^2=AB^2+BC^2\)
mà AB=BC nên ta có :
\(\Leftrightarrow\left(5\sqrt{2}\right)^2=AB^2+AB^2\)
\(\Leftrightarrow50=2AB^2\)
\(\Leftrightarrow AB^2=50:2=25\)
\(\Leftrightarrow AB=\sqrt{25}=5\)( đơn vị diện tích theo đề bạn )
\(S_{hìnhvuông}=a^2=5^2=25\)
còn 1 cách nữa nhưng cách này dễ hiểu hơn á .
PA
2
9 tháng 5 2022
Một cạnh của hình vuông là:
\(\dfrac{15}{7}\):4 = \(\dfrac{15}{28}\)(m)
Diện Tích là:
\(\dfrac{15}{28}\)x\(\dfrac{15}{28}\)=...(m2)
Đáp số .... m2
Còn lại em tự làm nhé
HK
23 tháng 4 2020
Bán kính của bánh xe đó là: 0,6 : 2 = 0,3 (m)
Diện tích bánh xe là: 0,3 x 0,3 x 3,14 = 0,2826 (cm2)
Quãng đường bánh xe lăn được 15 vòng là: 0,2826 x 15 = 4,239 (m)
20 vòng là: 0,2826 x 20 = 5,652 (m)
Đáp số:...
Tham khảo nha!!!
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 4 2022
\(I=\int\limits^{\dfrac{\pi}{2}}_0\left(1+cosx+x.cosx\right)e^{sinx}dx=\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx+\int\limits^{\dfrac{\pi}{2}}_0\left(x+1\right).cosx.e^{sinx}dx=I_1+I_2\)
Xét \(I_2\), đặt \(\left\{{}\begin{matrix}u=x+1\\dv=cosx.e^{sinx}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^{sinx}\end{matrix}\right.\)
\(\Rightarrow I_2=\left(x+1\right).e^{sinx}|^{\dfrac{\pi}{2}}_0-\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx=\left(\dfrac{\pi}{2}+1\right)e-1-I_1\)
\(\Rightarrow I=I_1+\left(\dfrac{\pi}{2}+1\right)e-1-I_1=\left(\dfrac{\pi}{2}+1\right)e-1\)
21 tháng 3 2023
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
\(C_2H_2+2Br_2\rightarrow C_2H_2Br_4\)
Ta có: \(n_{C_2H_4}+n_{C_2H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\left(1\right)\)
Theo PT: \(n_{Br_2}=n_{C_2H_4}+2n_{C_2H_2}=\dfrac{8}{160}=0,05\left(mol\right)\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_4}=0,55\\n_{C_2H_2}=-0,25\end{matrix}\right.\)
Đến đây thì ra số mol âm, bạn xem lại đề nhé.
Giao điểm của 2 pt đường tròn \(\left(\dfrac{\sqrt{3}}{2};\dfrac{1}{2}\right)\)
\(\left\{{}\begin{matrix}x=r\cos\varphi\\y=r\sin\varphi\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}r\in\left[2\sin\varphi;1\right]\\\varphi\in\left[0;\dfrac{\pi}{6}\right]\\\left|J\right|=r\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^{\dfrac{\pi}{6}}_0d\varphi\int\limits^1_{2\sin\varphi}\sqrt{r^2}.rdr=\int\limits^{\dfrac{\pi}{6}}_0d\varphi\int\limits^1_{2\sin\varphi}r^2dr=\dfrac{1}{3}\int\limits^{\dfrac{\pi}{6}}_0\left(1-8\sin^3\varphi\right)d\varphi=...\)