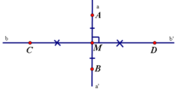
Trên đường thẳng AA' lấy điểm O nằm giữa A và A'. Trên một nữa mặt phẳng bờ AA', vẽ tia OB sao cho \(\widehat{AOB}\) = 45* (45 độ). Trên nửa mặt phẳng còn lại vẽ tia OC sao cho \(\widehat{AOC}\) = 90* (90 độ).
a) Gọi OB' là tia phân giác của \(\widehat{A'OC}\). Chứng tỏ rằng \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là hai góc đối đỉnh.
b) Trên nửa mặt phẳng bờ AA' có chứa tia OB, vẽ tia OD sao cho \(\widehat{DOB}\) = 90* (90 độ). Tính \(\widehat{A'OD}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.


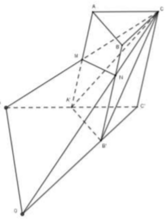
Sử dụng công thức tính thể tích khối chóp V = 1 3 h . S với h là chiều cao hình chóp và S là diện tích đáy.
Công thức tính thể tích lăng trụ V = h.S với h là chiều cao hìnhlăng trụ và S là diện tích đáy.
Cách giải:

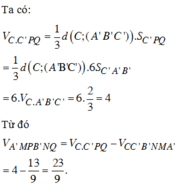

a a' o b c b'
ta có aoa'=aoc+a'oc
=>a'oc=180o-90o=90o
vì ob' là tia phân giác của a'oc
=>a'ob'=b'oc=1/2.a'oc=45o
aoa'=aob+a'ob
=>a'ob=aoa'-aob
=180o-45o=135o
vì ob và ob' nàm trên 2 nửa mặt phẳng đối nhau
=>a'ob+a'ob'=bob'=135o+45o=180o
bb' là 1 đường thẳng
aa' và bb' là 2 đường thẳng cắt nhau=>a'ob và aob' là 2 góc đối đỉnh
=>đpcm

rõ ràng là bạn không nên đùa rằng đề toán của bạn là ngữ văn 6 chứ
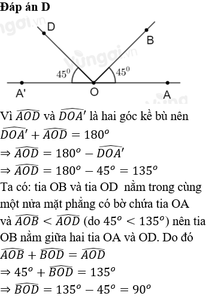
a) Vì OB' là tia phân giác của \(\widehat{A'OC}\) nên \(\widehat{A'OB'}=\dfrac{\widehat{A'OC}}{2}=\dfrac{90^o}{2}=45^o\). Suy ra \(\widehat{AOB}=\widehat{A'OB'}\left(=45^o\right)\). Lại có \(\widehat{AOB}+\widehat{BOA'}=\widehat{AOA'}=180^o\) nên \(\widehat{BOB'}=\widehat{A'OB'}+\widehat{BOA'}=180^o\) hay B, O, B' thẳng hàng. Suy ra \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là 2 góc đối đỉnh.
b) Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AA', ta thấy tia OB nằm giữa 2 tia OA và OD, tia OD lại nằm giữa 2 tia OB và OA', do đó \(\widehat{AOB}+\widehat{BOD}+\widehat{DOA'}=\widehat{AOA'}\) \(\Leftrightarrow45^o+90^o+\widehat{A'OD}=180^o\) \(\Leftrightarrow\widehat{A'OD}=45^o\)