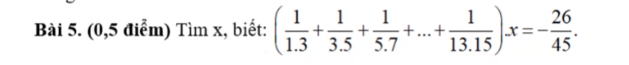Mình cần gấp mn ơi!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VD
17 tháng 3 2022
\(\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{13.15}\right).x=\dfrac{-26}{45}\\ \Leftrightarrow\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{13.15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{13}-\dfrac{1}{15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\left(1-\dfrac{1}{15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\dfrac{14}{15}.x=\dfrac{-52}{45}\\ \Leftrightarrow x=-\dfrac{26}{21}\)
17 tháng 3 2022
(11.3+13.5+...+113.15).x=−2645⇔(21.3+23.5+...+213.15).x=−5245⇔(1−13+13−15+...+113−115).x=−5245⇔(1−115).x=−5245⇔1415.x=−5245⇔x=−2621
H9
HT.Phong (9A5)
CTVHS
27 tháng 4 2023
3. Tóm tắt:
\(m_1=1,5kg\)
\(t_1=100^oC\)
\(m_2=200g=0,2kg\)
\(m_3=2,5kg\)
\(t_2=20^oC\)
\(c_1=380J/kg.K\)
\(c_2=880J/kg.K\)
\(c_3=4200J/kg.K\)
===========
a) \(t=?^oC\)
b) \(t'=70^oC\)
\(Q'=?J\)
Giải:
a) Nhiệt độ cuối cùng của nước:
\(Q_1=Q_2+Q_3\)
\(\Leftrightarrow m_1.c_1.\left(t_1-t\right)=\left(t-t_2\right)\left(m_2.c_2+m_3.c_3\right)\)
\(\Leftrightarrow1,5.380.\left(100-t\right)=\left(t-20\right)\left(0,2.880+2,5.4200\right)\)
\(\Leftrightarrow57000-570t=10676t-213520\)
\(\Leftrightarrow57000+213520=10676t+570t\)
\(\Leftrightarrow270520=11246t\)
\(\Leftrightarrow t=\dfrac{270520}{11246}=24,05^oC\)
b) Nhiệt lượng cần cung cấp để đun nóng nước:
\(Q'=\left(m_1.c_1+m_2.c_2+m_3.c_3\right).\left(t'-t\right)\)
\(\Leftrightarrow Q'=\left(1,5.880+0,2.880+2,5.4200\right)\left(70-24,05\right)\)
\(\Leftrightarrow Q'=11246.45,95\)
\(\Leftrightarrow Q'=516753,7J\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 4 2023
1. Tóm tắt:
\(m=300kg\)
\(\Rightarrow P=10m=3000N\)
\(h=1,5m\)
\(s=6m\)
\(F=1250N\)
==========
a) \(A_i=?J\)
b) \(A_{tp}=?J\)
c) \(H=?\%\)
\(F_{ms}=?N\)
Giải:
a) Công có ích thực hiện được:
\(A_i=P.h=3000.1,5=4500J\)
b) Công toàn phần thực hiện được:
\(A_{tp}=F.s=1250.6=7500J\)
c) Hiệu suất mặt phẳng nghiêng:
\(H=\dfrac{A_i}{A_{tp}}.100\%=\dfrac{4500}{7500}.100\%=60\%\)
Công của lực ma sát:
\(A_{ms}=A_{tp}-A_i=7500-4500=3000J\)
Độ lớn của lực ma sát:
\(A_{ms}=F_{ms}.s\Rightarrow F_{ms}=\dfrac{A_{ms}}{s}=\dfrac{3000}{6}=500N\)
ND
1
MN
24 tháng 8 2021
\(2xR+yO_2\underrightarrow{^{^{t^0}}}2R_xO_y\)
\(2KMnO_4+16HCl_{\left(đ\right)}\underrightarrow{^{^{t^0}}}2KCl+2MnCl_2+5Cl_2+8H_2O\)
\(C_nH_{2n+2}+\dfrac{3n+1}{2}O_2\underrightarrow{^{^{t^0}}}nCO_2+\left(n+1\right)H_2O\)
\(8Al+30HNO_3\rightarrow8Al\left(NO_3\right)_3+3N_2O+15H_2O\)
25 tháng 10 2021
\(a,A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\\ b,A=\dfrac{2\left(\sqrt{x}+1\right)-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\sqrt{x}+1\inƯ\left(3\right)=\left\{1;3\right\}\left(\sqrt{x}+1\ge1\right)\\ \Leftrightarrow\sqrt{x}\in\left\{0;2\right\}\\ \Leftrightarrow x\in\left\{0;4\right\}\left(tm\right)\)
25 tháng 10 2021
a) \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(\Rightarrow A=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2x-2\sqrt{x}\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)