Tam giác ABC có AB/5 BC/12=AC/13 có phải tam giác vuông không
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1
MN
18 tháng 2 2021
\(TC:\)
\(BC^2=15^2=225\)
\(AB^2+AC^2=9^2+12^2=255\)
\(\Rightarrow BC^2=AB^2+AC^2\)
\(\Rightarrow\Delta ABC\perp A\)
18 tháng 2 2021
Vì AB,AC,BC tỉ lệ với 9;12;15 nên \(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)
Đặt \(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}=k\)
nên \(\left\{{}\begin{matrix}AB=9k\\AC=12k\\BC=15k\end{matrix}\right.\)
Vì \(\left(15k\right)^2=\left(9k\right)^2+\left(12k\right)^2\)
nên \(BC^2=AB^2+AC^2\)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
MH
5 tháng 2 2022
Ta có các cạnh AB; AC; BC tỉ lệ với 9; 12 và 15
⇒ \(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)
Đặt \(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}=k\)
⇒ \(\left\{{}\begin{matrix}AB=9k\\AC=12k\\BC=15k\end{matrix}\right.\)
Ta có:
\(AB^2+AC^2=BC^2\)
\(\left(9k\right)^2+\left(12k\right)^2=\left(15k\right)^2\)
\(81k^2+144k^2=225k^2\)
\(225k^2=225k^2\)
Áp dụng định lý Pytago đảo
⇒ Tam giác ABC vuông tại A
LT
1
30 tháng 10 2023
Xét ΔABC có \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
N
1
25 tháng 1 2022
Đặt AB/9=AC/12=BC/15=k
=>AB=9k; AC=12k; BC=15k
Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
KV
3 tháng 5 2023
Tổng độ dài hai cạnh AB và AC:
30 - 13 = 17 (cm)
Tổng số phần bằng nhau:
5 + 12 = 17 (phần)
Cạnh AB dài:
17 . 5 : 17 = 5 (cm)
Cạnh AC dài:
17 . 12 : 17 = 12 (cm)
Diện tích tam giác ABC:
5 . 12 : 2 = 30 (cm²)
3 tháng 5 2023
Tổng độ dài 2 đáy AB và AC là :
30 - 13 = 17 ( cm )
Tổng số phần bằng nhau là
5 + 12 = 17 ( phần )
Cạnh AB dài là
17 : 17 x 5 = 5 ( cm )
Cạnh AC dài là :
17 - 5 = 12 ( cm )
Diện tích hình tam giác vuông ABC là
12 x 5 : 2 = 30 ( m2)
Đáp số : 30 m2
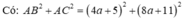
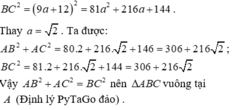
Ta có: \(\dfrac{AB}{5}=\dfrac{BC}{12}=\dfrac{AC}{13}=k\)
\(\Rightarrow AB=5k,BC=12k,AC=13k\)
Mà: Cạnh có độ dài dài nhất chính là cạnh huyền:
Vậy \(\Rightarrow AC=13k\) là cạnh huyền
\(\Rightarrow AC^2=AB^2+BC^2\)
Hay: \(\left(13k\right)^2=\left(5k\right)^2+12k^2\)
\(\Leftrightarrow169k^2=25k^2+144k^2=169k^2\) (đúng)
Vậy tam giác là tam giác vuông tại B