Một chất điểm dao động điều hòa với biên độ 4cm, tần số bằng 2Hz. Giữa hai lần liên tiếp chất điểm có tốc độ bằng 8π√3 cm/s, tốc độ chuyển động trung bình của chất điểm bằng ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để tính biên độ của chất điểm dao động điều hòa, ta có thể sử dụng công thức vận tốc trung bình trong một chu kỳ dao động:
v_trung_binh = (2πA) / T
Trong đó: v_trung_binh là vận tốc trung bình của chất điểm trong một chu kỳ (cm/s) A là biên độ của chất điểm (cm) T là chu kỳ của dao động (s)
Theo đề bài, vận tốc trung bình trong khoảng thời gian từ t = 2,8 s đến t = 3,6 s là 10 cm/s. Ta cũng biết rằng vận tốc của chất điểm bằng 0 tại hai thời điểm liên tiếp t = 2,8 s và t = 3,6 s. Điều này có nghĩa là chất điểm đã hoàn thành một nửa chu kỳ dao động trong khoảng thời gian đó.
Từ đó, ta có thể suy ra được chu kỳ của dao động:
T = 2 * (3,6 - 2,8) = 1,6 s
Tiếp theo, ta có thể sử dụng công thức vận tốc trung bình để tính biên độ:
10 = (2πA) / 1,6
Từ đó, ta có:
A = (10 * 1,6) / (2π) ≈ 2,54 cm
Vậy, biên độ của chất điểm dao động là khoảng 2,54 cm.

Chọn B.
Vận tốc cực đại: v m a x = ω A = 2 πfA = 8 ( cm / s )



Ta có: \(f=2Hz\)
\(\Rightarrow\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{1}{f}}=4\pi\left(rad/s\right)\)
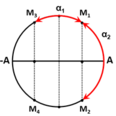
\(x=\pm\sqrt{A^2-\left(\dfrac{v}{\omega}\right)^2}=\pm\sqrt{4^2-\left(\dfrac{8\pi\sqrt{3}}{4\pi}\right)^2}=\pm2\left(cm\right)\)
TH1:
\(s=2x=2\cdot2=4\left(cm\right)\)
\(t_1=\dfrac{T}{12}+\dfrac{T}{12}=\dfrac{\dfrac{1}{f}}{12}+\dfrac{\dfrac{1}{f}}{12}=\dfrac{\dfrac{1}{2}}{12}+\dfrac{\dfrac{1}{2}}{12}=\dfrac{1}{12}\left(s\right)\)
\(\Rightarrow v_{tb1}=\dfrac{4}{\dfrac{1}{12}}=\dfrac{48}{1}=48\left(cm/s\right)\)
TH2:
\(s=2x=2\cdot2=4\left(cm\right)\)
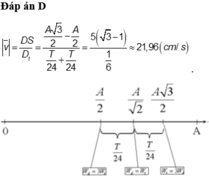
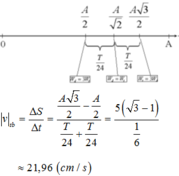
\(t_2=\dfrac{T}{6}+\dfrac{T}{6}=\dfrac{\dfrac{1}{f}}{6}+\dfrac{\dfrac{1}{f}}{6}=\dfrac{\dfrac{1}{2}}{6}+\dfrac{\dfrac{1}{2}}{6}=\dfrac{1}{6}\left(s\right)\)
\(\Rightarrow v_{tb2}=\dfrac{s}{t_2}=\dfrac{4}{\dfrac{1}{6}}=\dfrac{24}{1}=24\left(cm/s\right)\)
Ta áp dụng công thức : \(V=2\pi\dfrac{A}{T}\)
Chu kỳ chuyển động của nó là:
\(T=\dfrac{1}{F}=\dfrac{1}{2}=0,5\left(s\right)\)
Tốc độ chuyển động trung bình của nó là:
\(V=2\pi\dfrac{4}{0,5}=8\pi\left(cm/s\right)\)
đ/s:.......