tìm đkxđ √24+10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KR
1
24 tháng 10 2021
a: ĐKXĐ: \(x\ne-1\)
b: \(B=\dfrac{5}{x+1}+\dfrac{10}{x^2-x+1}-\dfrac{15}{x^3-1}\)
\(=\dfrac{5x^2-5x+5+10x+10-15}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{5x^2+5x}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{5x}{x^2-x+1}\)
7 tháng 12 2021
\(a,ĐK:x\ne2\\ b,A=\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3}{x-2}\\ c,x=\dfrac{2021}{1010}\Leftrightarrow A=\dfrac{3}{\dfrac{2021}{1010}-\dfrac{2020}{1010}}=\dfrac{3}{\dfrac{1}{1010}}=3030\)
30 tháng 12 2021
a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
\(C=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
LK
0
31 tháng 10 2021
\(1,\\ a,ĐK:\left\{{}\begin{matrix}x\ge0\\x+5\ge0\end{matrix}\right.\Leftrightarrow x\ge0\\ b,Sửa:B=\left(\sqrt{3}-1\right)^2+\dfrac{24-2\sqrt{3}}{\sqrt{2}-1}\\ B=4-2\sqrt{3}+\dfrac{2\sqrt{3}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}\\ B=4-2\sqrt{3}+2\sqrt{3}=4\\ 3,\\ =\left[1-\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{1+\sqrt{x}}\right]\cdot\dfrac{\sqrt{x}-3+2-2\sqrt{x}}{\left(1-\sqrt{x}\right)\left(\sqrt{x}-3\right)}-2\\ =\left(1-\sqrt{x}\right)\cdot\dfrac{-\sqrt{x}-1}{\left(1-\sqrt{x}\right)\left(\sqrt{x}-3\right)}-2\\ =\dfrac{-\sqrt{x}-1}{\sqrt{x}-3}-2=\dfrac{-\sqrt{x}-1-2\sqrt{x}+6}{\sqrt{x}-3}=\dfrac{-3\sqrt{x}+5}{\sqrt{x}-3}\)
10 tháng 1 2024
a: ĐKXĐ: \(x^2+y^2\ne0\)
=>\(\left[{}\begin{matrix}x^2\ne0\\y^2\ne0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
b: ĐKXĐ: \(x^2-2x+1\ne0\)
=>\(\left(x-1\right)^2\ne0\)
=>\(x-1\ne0\)
=>\(x\ne1\)
c: ĐKXĐ: \(x^2+6x+10\ne0\)
=>\(x^2+6x+9+1\ne0\)
=>\(\left(x+3\right)^2+1\ne0\)(luôn đúng)
d:ĐKXĐ: \(\left(x+3\right)^2+\left(y-2\right)^2\ne0\)
=>\(\left[{}\begin{matrix}x+3\ne0\\y-2\ne0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x\ne-3\\y\ne2\end{matrix}\right.\)
GH
8 tháng 7 2023
Để \(\sqrt{\dfrac{2\sqrt{15}-\sqrt{59}}{x-7}}\) được xác định thì \(\dfrac{2\sqrt{15}-\sqrt{59}}{x-7}\ge0\)
\(\Leftrightarrow x-7>0\\ \Leftrightarrow x>7\)
Để \(\sqrt{\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}}\) được xác định thì \(\dfrac{-2\sqrt{6}+\sqrt{23}}{-x+5}\ge0\)
\(\Leftrightarrow-x+5< 0\\ \Leftrightarrow x>5\)
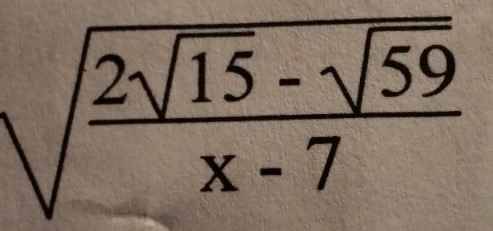
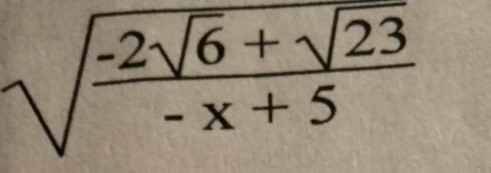
Vì các số trong căn bậc `2` không âm nên căn thức được xác định.