2. Xác định các hệ số a,b,c Tính biệt thức từ đó áp dụng công thức nghiệm để giải các pt sau:
a. \(3x^2-4x+1=0\)
b. \(-4x^2+4x+1=0\)
d. \(x^2-\sqrt{8}x+2=0\)
e. \(x^2-6x+5=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình bậc hai: 7x2 – 2x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b2 – 4ac = (-2)2 – 4.7.3 = -80 < 0
Vậy phương trình vô nghiệm.

Phương trình bậc hai 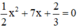
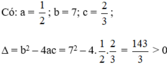
Vậy phương trình có hai nghiệm phân biệt.

Phương trình bậc hai 1,7x2 – 1,2x – 2,1 = 0
Có: a = 1,7; b = -1,2; c = -2,1; Δ = b2 – 4ac = (-1,2)2 – 4.1,7.(-2,1) = 15,72 > 0
Vậy phương trình có hai nghiệm phân biệt.

a) Phương trình bậc hai: 7 x 2 – 2 x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b 2 – 4 a c = ( - 2 ) 2 – 4 . 7 . 3 = - 80 < 0
Vậy phương trình vô nghiệm.
b) Phương trình bậc hai 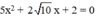
Có: a = 5; b = 2√10; c = 2; Δ = b 2 – 4 a c = ( 2 √ 10 ) 2 – 4 . 2 . 5 = 0
Vậy phương trình có nghiệm kép.
c) Phương trình bậc hai 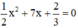
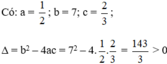
Vậy phương trình có hai nghiệm phân biệt.
d) Phương trình bậc hai 1 , 7 x 2 – 1 , 2 x – 2 , 1 = 0
Có: a = 1,7; b = -1,2; c = -2,1;
Δ = b 2 – 4 a c = ( - 1 , 2 ) 2 – 4 . 1 , 7 . ( - 2 , 1 ) = 15 , 72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 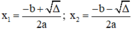
+ Nếu Δ = 0, phương trình có nghiệm kép 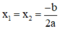 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.

Phương trình 2 x 2 – 5x + 1 = 0 có a = 2, b = -5, c = 1
Ta có: ∆ = b 2 – 4ac = - 5 2 – 4.2.1 = 25 – 8 = 17 > 0
∆ = 17
Phương trình có 2 nghiệm phân biệt :
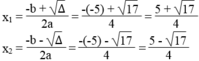

Phương trình 5 x 2 – x + 2 = 0 có a = 5, b = -1, c = 2
Ta có: ∆ = b 2 – 4ac = - 1 2 – 4.5.2 = 1 – 40 = -39 < 0
Vậy phương trình vô nghiệm.

Phương trình -3 x 2 + 2x + 8 = 0 có a = -3, b = 2, c = 8
Ta có: Δ = b 2 – 4ac = 2 2 – 4.(-3).8 = 4 + 96 = 100 > 0
∆ = 100 = 10
Phương trình có 2 nghiệm phân biệt :
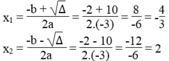

Phương trình 4 x 2 + 4x + 1 = 0 có a = 4, b = 4, c = 1
Ta có: ∆ = b 2 – 4ac = 4 2 – 4.4.1 = 16 – 16 = 0
Phương trình có nghiệm kép :


a
a = 1, b = -3, c = 2
\(\Delta=b^2-4ac=\left(-3\right)^2-4.1.2=9-8=1\)
Nhẩm nghiệm:
a + b + c = 0 (1 - 3 + 2 = 0)
\(\Rightarrow x_1=1;x_2=\dfrac{c}{a}=\dfrac{2}{1}=2\)
b
a = -2, b = 1, c = 1
\(\Delta=1^2-4.\left(-2\right).1=1+8=9\)
Nhẩm nghiệm:
a + b + c = 0 (-2 + 1 + 1 = 0)
\(\Rightarrow x_1=1;x_2=\dfrac{c}{a}=\dfrac{1}{-2}=-\dfrac{1}{2}\)
c
a = 1, b = -4, c = 4
\(\Delta=\left(-4\right)^2-4.4=16-16=0\)
=> Phương trình có nghiệm kép.
\(x_1=x_2=-\dfrac{b}{2a}=\dfrac{-4}{2.1}=-2\)
d
a = 1, b = -1, c = 4
\(\Delta=\left(-1\right)^2-4.4=1-16=-15< 0\)
=> Phương trình vô nghiệm.
a) x² - 3x + 2 = 0
a = 1; b = -3; c = 2
∆ = b² - 4ac = (-3)² - 4.1.2 = 9 - 8 = 1 > 0
Phương trình có hai nghiệm phân biệt:
x₁ = (-b + √∆)/2a = [-(-3) + 1]/2 = 2
x₂ = (-b - √∆)/2a = [-(-3) - 1]/2 = 1
Vậy S = {1; 2}
b) -2x² + x + 1 = 0
a = -2; b = 1; c = 1
∆ = b² - 4ac = 1² - 4.(-2).1 = 9 > 0
Phương trình có hai nghiệm phân biệt
x₁ = (-b + √∆)/2a = (-1 + 3)/[2.(-2)] = -1/2
x₂ = (-b - √∆)/2a = (-1 - 3)/[2.(-2)] = 1
Vậy S = {-1/2; 1}
c) x² - 4x + 4 = 0
a = 1; b = -4; c = 4
∆ = b² - 4ac = (-4)² - 4.1.4 = 0
Phương trình có nghiệm kép:
x₁ = x₂ = -b/2a = -(-4)/(2.1) = 2
Vậy S = {2}
d) x² - x + 4 = 0
a = 1; b = -1; c = 4
∆ = b² - 4ac = (-1)² - 4.1.4 = -15 < 0
Phương trình vô nghiệm
a) 3x² - 4x + 1 = 0
a = 3; b = -4; c = 1
∆ = b² - 4ac = (-4)² - 4.3.1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
x₁ = (-b + √∆)/2a = [-(-4) + 2]/(2.3) = 1
x₂ = (-b - √∆)/2a = [-(-4) - 2]/(2.3) = 1/3
Vậy S = {1/3; 1}
b) -4x² + 4x + 1 = 0
a = -4; b = 4; c = 1
∆ = b² - 4ac = 4² - 4.(-4).1 = 32 > 0
Phương trình có hai nghiệm phân biệt:
x₁ = (-b + √∆)/2a = (-4 + 4√2)/[2.(-4)] = (1 - √2)/2
x₂ = (-b - √∆)/2a = (-4 - 4√2)/[2.(-4)] = (1 + √2)/2
Vậy S = {(1 - √2)/2; (1 + √2)/2}
d) x² - 8x + 2 = 0
a = 1; b = -√8; c = 2
∆ = b² - 4ac = 8 - 8 = 0
Phương trình có nghiệm kép:
x₁ = x₂ = -b/2a = √8/2 = √2
Vậy S = {√2}
e) x² - 6x + 5 = 0
a = 1; b = -6; c = 5
∆ = b² - 4ac = 36 - 20 = 16 > 0
Phương trình có hai nghiệm phân biệt:
x₁ = (-b + √∆)/2a = (6 + 4)/2 = 5
x₂ = (-b - √∆)/2a = (6 - 4)/2 = 1
Vậy S = {1; 5}
Bạn nên viết đề bằng công thức toán để mọi người dễ đọc hơn nhé (nhấn vào biểu tượng $\sum$ góc trái khung soạn thảo)