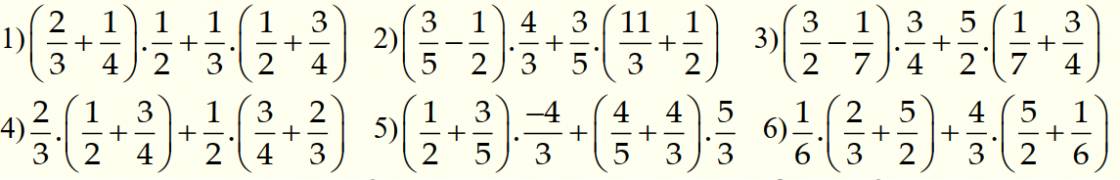
Tính:
Mọi người giúp mik với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 12 2022
\(a,=\dfrac{x^3+2x}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}=\dfrac{x^3+2x+2x-2-\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3+3}{\left(x^2+x+1\right)}\)
NH
2
AH
Akai Haruma
Giáo viên
13 tháng 11 2023
Bài 1:
$0,2-\frac{4}{7}+\frac{-6}{5}=\frac{1}{5}+\frac{-6}{5}-\frac{4}{7}$
$=\frac{-5}{5}-\frac{4}{7}=-1-\frac{4}{7}=\frac{-11}{7}$
b.
$=(\frac{-2}{3})^2+\frac{5}{6}+(-1)=\frac{4}{9}+\frac{5}{6}-1$
$=\frac{8}{18}+\frac{15}{18}-1=\frac{23}{18}-1=\frac{5}{18}$
c.
$=1+3+5+7+9=25$
AH
Akai Haruma
Giáo viên
13 tháng 11 2023
Bài 2:
a. $-(0,5+x)-\frac{1}{3}=\frac{1}{6}$
$-(0,5+x)=\frac{1}{3}+\frac{1}{6}=\frac{1}{2}$
$0,5+x=\frac{-1}{2}$
$x=\frac{-1}{2}-0,5=-1$
b.
$(x+\frac{4}{9})(x-\frac{11}{5})=0$
$\Rightarrow x+\frac{4}{9}=0$ hoặc $x-\frac{11}{5}=0$
$\Rightarrow x=\frac{-4}{9}$ hoặc $x=\frac{11}{5}$
c.
$\frac{1}{3}-|\frac{5}{4}-2x|=\frac{1}{4}$
$|\frac{5}{4}-2x|=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}$
$\Rightarrow \frac{5}{4}-2x=\frac{1}{12}$ hoặc $\frac{5}{4}-2x=\frac{-1}{12}$
$\Rightarrow x=\frac{1}{2}(\frac{5}{4}-\frac{1}{12})$ hoặc $x=\frac{1}{2}(\frac{5}{4}+\frac{1}{12})$
$\Rightarrow x=\frac{7}{12}$ hoặc $x=\frac{2}{3}$
10 tháng 1 2023
a: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
b: \(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
c: \(=\dfrac{6-7+x}{3\left(x-1\right)}=\dfrac{x-1}{3\left(x-1\right)}=\dfrac{1}{3}\)
d: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
NU
3
MH
10 tháng 5 2022
\(=82\times\left(10,5+3,2\right)+13,7\times18\)
\(=13,7\times82+18\times13,7\)
\(=13,7\times\left(18+82\right)\)
\(=13,7\times100=1370\)
DX
17 tháng 12 2022
11)\(\dfrac{3x+1}{x-5}+\dfrac{2x}{x-5}=\dfrac{3x+2x+1}{x-5}=\dfrac{5x+1}{x-5}\)
12)\(\dfrac{4-x^2}{x-3}+\dfrac{2}{x^2-9}=\dfrac{4-x^2}{x-3}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(4-x^2\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{2}{\left(x-3\right)\left(x+3\right)}=\dfrac{2+\left(2-x\right)\left(2+x\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
13)
\(\dfrac{3}{4x-2}+\dfrac{2x}{4x^2-1}=\dfrac{3}{2\left(2x-1\right)}+\dfrac{2x}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{3\left(2x+1\right)}{2\left(2x-1\right)\left(2x+1\right)}+\dfrac{2.2x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{6x+3+4x}{2\left(2x-1\right)\left(2x+1\right)}=\dfrac{10x+3}{2\left(2x-1\right)\left(2x+1\right)}\)
14)
\(\dfrac{2x+1}{2x-4}+\dfrac{5}{x^2-4}=\dfrac{2x+1}{2\left(x-2\right)}+\dfrac{5}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(2x+1\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\dfrac{5.2}{2\left(x-2\right)\left(x+2\right)}=\dfrac{2x^2+5x+12}{2\left(x-2\right)\left(x+2\right)}\)
NN
0
6 tháng 1 2022
Ta có:
\(C=\dfrac{2n-3}{n-2}=\dfrac{2n-4+1}{n-2}=2+\dfrac{1}{n-2}\)
\(C\in Z\Leftrightarrow\dfrac{1}{n-2}\in Z\Leftrightarrow n-2\inƯ\left(1\right)=\left\{-1;1\right\}\)
\(\Rightarrow...\)