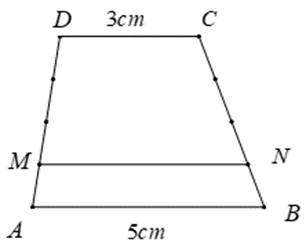
Cho hình thang ABCD có độ dài đáy AB=5cm; CD=3cm. Các điểm M, N lần lượt nằm trên các cạnh AD và BC sao cho MA= 1/4 AD, NB= 1/4BC. Nối M với N, ta được hai hình thang ABNM và CDMN. S của ABCD =16cm2. Tính độ dài MN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 12 2023
a: \(CD=3\cdot AB=3\cdot4=12\left(cm\right)\)
b: Diện tích hình thang ABCD là:
\(S_{ABCD}=\dfrac{1}{2}\cdot\left(AB+CD\right)\cdot AH=\dfrac{1}{2}\cdot3\cdot\left(12+4\right)=\dfrac{3}{2}\cdot16=24\left(cm^2\right)\)
c: ABCD là hình thang cân
=>AD=BC
mà AD=5cm
nên BC=5cm
Chu vi hình thang ABCD là:
\(C_{ABCD}=AB+BC+CD+DA\)
=5+5+4+12
=10+16
=26(cm)
CM
10 tháng 5 2019
Đáp án cần chọn là: A.
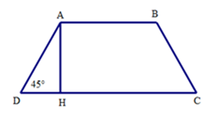
Ta có tam giác ADH vuông cân tại H vì D ^ = 45 ° .
Do đó DH = AH = 5cm
Mà DH = 1 2 (CD – AB)
Suy ra CD = 2DH + AB = 2.5 + 3 = 13 (cm)
Vậy CD = 13 cm
HC
15 tháng 1 2015
Mình nghĩ rằng bạn bị nhầm đề. Nếu là cạnh AC = 8cm ( có như thế thì mới tìm được liên hệ về độ dài các cạnh là bội số của tam giác vuông) => kq =24 cm2. Cách giải sẽ là: Gọi I, K tương ứng là trung điểm của AD, BC. Lúc đó MIN, MKN là 2 tam giác vuông tại I, K. MINK là hcn. SABCD = 2SMINK= 4SMIN= 24 cm2.
16 tháng 10 2018
Bạn lầu trên ơi, 2 đường chéo có vuông góc vs nhau đâu mà ta có 2 tam giác vuông đó nhỉ.
6 tháng 11 2021
Bài 1:
\(S=\dfrac{12+20}{2}\cdot8=16\cdot8=128\left(cm^2\right)\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 12 2024
Bài 2:
Vì ABCD là hình thang cân (gt)
Suy ra: BD = AC (hình thang cân có hai đường chéo bằng nhau)
BD = 5cm (gt)
AC = 3cm (gt)
5cm > 3cm
Suy ra BD > AC (vô lí)
Vậy không tồn tại hình thang cân nào thỏa mãn đề bài.
A B C D M N
Hai tg ACD và tg ABC có đường cao từ A->CD = đường cao từ C->AB nên
\(\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{CD}{AB}=\dfrac{3}{5}\)
\(S_{ABCD}=S_{ACD}+S_{BCD}\)
\(\Rightarrow S_{ACD}=\dfrac{3}{3+5}xS_{ABCD}=\dfrac{3}{8}xS_{ABCD}=\dfrac{3}{8}x16=6cm^2\)
\(\Rightarrow S_{ABC}=S_{ABCD}-S_{ACD}=16-6=10cm^2\)
Hai tg ACD và tg BCD có đường cao từ A->CD = đường cao từ B->CD và chung cạnh CD
\(\Rightarrow S_{ACD}=S_{BCD}=6cm^2\)
C/m tương tự ta cũng có
\(S_{ABC}=S_{ABD}=10cm^2\)
Hai tg ABN và tg ABC có chung đường cao từ A->BC nên
\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{BN}{BC}=\dfrac{1}{4}\Rightarrow S_{ABN}=\dfrac{1}{4}xS_{ABC}=\dfrac{1}{4}x10=2,5cm^2\)
đường cao từ N->AB là
\(\dfrac{2xS_{ABN}}{AB}=\dfrac{2x2,5}{5}=1cm\)
Hai tg NCD và tg BCD có chung đường cao từ D->BC nên
\(\dfrac{S_{NCD}}{S_{BCD}}=\dfrac{CN}{BC}=\dfrac{3}{4}\Rightarrow S_{NCD}=\dfrac{3}{4}xS_{BCD}=\dfrac{3}{4}x6=4,5cm^2\)
\(S_{ADN}=S_{ABCD}-S_{ABN}-S_{CDN}=16-2,5-4,5=9cm^2\)
Hai tg AMN và tg ADN có chung đường cao từ N->AD nên
\(\dfrac{S_{AMN}}{S_{ADN}}=\dfrac{AM}{AD}=\dfrac{1}{4}\Rightarrow S_{AMN}=\dfrac{1}{4}xS_{ADN}=\dfrac{1}{4}x9=2.25cm^2\)
\(S_{ABNM}=S_{ABN}+S_{AMN}=2,5+2,25=4,75cm^2\)
Như vậy ta biết diện tích hình thang ABNM, biết đáy lớn AB, biết đường cao (đường cao từ N->AB). Áp dụng công thức tính diện tích hình thang sẽ tính được đáy nhỏ MN.
Bạn tự tính nốt nhé
Sabcd = 16cm² => (3+5)xHabcd =32 cm => Habcd = 4cm.
Điểm M và N lần lượt = 1/4 AD và BC nên chiều cao ABNM = 4:4 = 1cm. Chiều cao CD đến MN = 4-1= 3cm
Ta có: Sabnm + Smncd = 16cm² => (5+mn)+ (3+mn)x3 = 32cm
4mn+14=32cm => mn=4,5cm