Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chứng minh AB=AC; DB=DM và EC=EM.
Chu vi ΔADE bằng
= AD + DM + ME + AE
= AD + DB + EC + AE
= AB + AC
= 2AB.
Ta có AB = AC; DB = DM;
EC = EM.
Chu vi Δ ADE:
AD +AE +DE = AD +DM + AE + EM
=AD + DB + AE + EC = AB + AC = 2AB
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)
Bạn tự vẽ hình nha
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // OI (OI là đường trung bình của tam giác BCD).
Vậy BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
AC^2 = OA^2 – OC^2 = 42 – 22 = 12
=> AC = √12 = 2√3 (cm)
\(\sin OAC=\frac{OC}{OA}=\frac{1}{2}\)
=> OAC =30 độ
mà BAC =2OAC
=. BAC =60
Tam giác ABC cân có BAC = 60 => Tam giác ABC đều
+> AB=AC=BC=2√3 (cm)
K cho mk nh
câu A : AB = AC ( theo tính chất của đường tiếp tuyến ) suy ra : tam giác ABC cân tại A , OA là đường phân giác cũng là đường cao vậy OA vuông góc với BC
Đáp án B
* Theo tính chất hai tiếp tuyến cắt nhau ta có:
AB = AC; DB = DM; EM = EC
suy ra: DE = DM + ME = DB + EC.
* Chu vi tam giác ADE là:
AD + AE + DE = AD + AE + DB + EC
= (AD + DB ) + ( AE + EC ) = AB + AC = 2AB ( vì AB = AC )
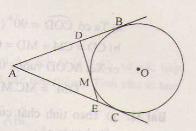
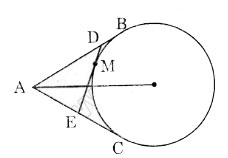
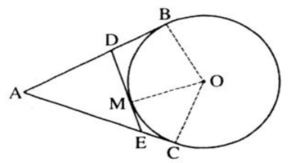
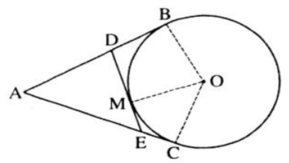
Ta có
DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)
\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)
\(=AB+AC=2AB\)
Theo tính chất hai tiếp tuyến cắt nhau ta có: DM=DB, EM=ECDM=DB,EM=EC.
Chu vi tam giác ADEADE bằng :
AD+DE+AE=AD+DM+ME+EAAD+DE+AE=AD+DM+ME+EA
=AD+DB+EC+AE=AD+DB+EC+AE
=AB+AC=2 . AB=AB+AC=2.AB .