Một ô tô khởi hành từ A đi đến B. Trên nửa quãng đường đầu, ô tô đi với vận tốc v1 = 30 km / h, nửa quãng đường sau ô tô đi với vận tốc v2. Vận tốc trung bình trên cả quãng đường là 37,5 km / h.
a. Tính vận tốc v2.
b. Nếu nửa thời gian (cần thiết đi từ A tới B) ôtô đi với vận tốc v1, nửa thời gian còn lại ôtô đi với vận tốc v2 thì vận tốc trung bình của ô tô trên cả quãng đường là bao...
Đọc tiếp
Một ô tô khởi hành từ A đi đến B. Trên nửa quãng đường đầu, ô tô đi với vận tốc v1 = 30 km / h, nửa quãng đường sau ô tô đi với vận tốc v2. Vận tốc trung bình trên cả quãng đường là 37,5 km / h.
a. Tính vận tốc v2.
b. Nếu nửa thời gian (cần thiết đi từ A tới B) ôtô đi với vận tốc v1, nửa thời gian còn lại ôtô đi với vận tốc v2 thì vận tốc trung bình của ô tô trên cả quãng đường là bao nhiêu?
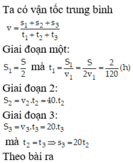
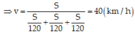
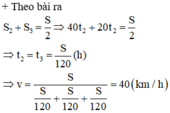
a) Vận tốc \(v_2\) là:
\(v_{tb}=\dfrac{s}{t_1+t_2}=\dfrac{s}{\dfrac{s}{2v_1}+\dfrac{s}{2v_2}}\Leftrightarrow\dfrac{1}{v_{tb}}=\dfrac{1}{2v_1}+\dfrac{1}{2v_2}\)
\(\Leftrightarrow\dfrac{1}{37,5}=\dfrac{1}{2\cdot30}+\dfrac{1}{2v_2}\Leftrightarrow\dfrac{1}{37,5}=\dfrac{1}{60}+\dfrac{1}{2v_2}\Leftrightarrow\dfrac{1}{100}=\dfrac{1}{2v_2}\Leftrightarrow v_2=\dfrac{100}{2}=50km/h\)
b) Vận tốc trung binhg trên cả quãng đường là:
\(v_{tb}'=\dfrac{s_1+s_2}{t}=\dfrac{v_1\dfrac{t}{2}+v_2\dfrac{t}{2}}{t}=\dfrac{v_1+v_2}{2}=\dfrac{30+50}{2}=\dfrac{80}{2}=40\left(km/h\right)\)