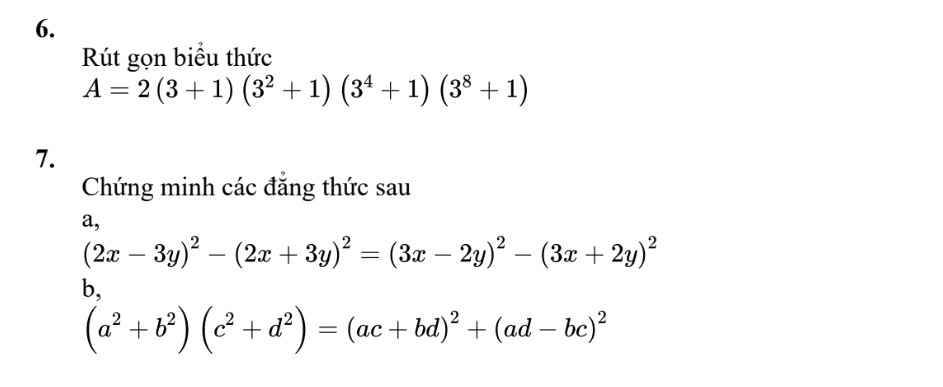
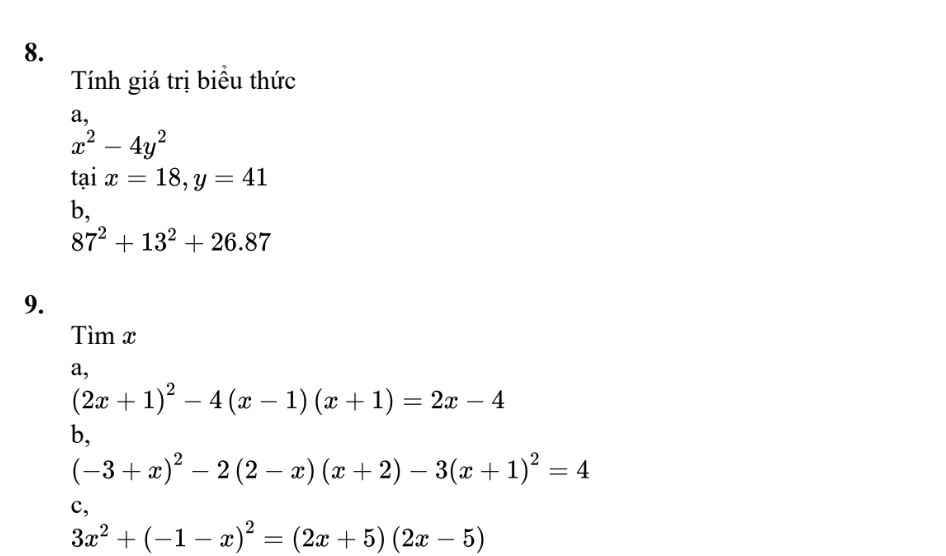
mn giúp mk gấp 7,8,9 vs mk (thank mn) :<
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BM
3
19 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`8,`
`a,`
Thay \(x=18;y=41\) vào bt
\(18^2-4\cdot41^2\)
`= 18^2 - (2*41)^2`
`= 18^2 - 82^2`
`= -6400`
`b,`
\(87^2+13^2+26\cdot87\)
`= 87*(87+26) + 169`
`= 87*113 + 169`
`= 9831 + 169`
`= 10000`
Y
19 tháng 6 2023
\(9,\) \(a,\left(2x+1\right)^2-4\left(x-1\right)\left(x+1\right)=2x-4\)
\(\Leftrightarrow4x^2+4x+1-4\left(x^2-1\right)-2x+4=0\)
\(\Leftrightarrow4x^2+4x+1-4x^2+4-2x+4=0\)
\(\Leftrightarrow\left(4x^2-4x^2\right)+\left(4x-2x\right)+\left(1+4+4\right)=0\)
\(\Leftrightarrow2x=-9\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy \(S=\left\{-\dfrac{9}{2}\right\}\)
\(b,\left(-3+x\right)^2-2\left(2-x\right)\left(x+2\right)-3\left(x+1\right)^2=4\)
\(\Leftrightarrow9-6x+x^2-2\left(2x+4-x^2-2x\right)-3\left(x^2+2x+1\right)-4=0\)
\(\Leftrightarrow9-6x+x^2-4x-8+2x^2+4x-3x^2-6x-3-4=0\)
\(\Leftrightarrow-12x=6\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)
\(c,3x^2+\left(-1-x\right)^2=\left(2x+5\right)\left(2x-5\right)\)
\(\Leftrightarrow3x^2+1+2x+x^2=4x^2-25\)
\(\Leftrightarrow2x=-26\)
\(\Leftrightarrow x=-13\)
Vậy \(S=\left\{-13\right\}\)
NH
0
QM
2
QM
1
QM
1
QM
1
1 tháng 7 2023
a: (x-4)(x+5)>0
=>x-4>0 hoặc x+5<0
=>x>4 hoặc x<-5
b: (2x+1)(x-3)<0
=>2x+1>0 và x-3<0
=>-1/2<x<3
c: (x-7)(3-x)<0
=>(x-7)(x-3)>0
=>x>7 hoặc x<3
d: x^2+6x-16<0
=>(x+8)(x-2)<0
=>-8<x<2
e: 3x^2+7x+4<0
=>3x^2+3x+4x+4<0
=>(x+1)(3x+4)<0
=>3x+4>0 và x+1<0
=>-4/3<x<-1
f: 5x^2-9x+4>0
=>(x-1)(5x-4)>0
=>x>1 hoặc x<4/5
g: x^2+6x-16<0
=>(x+8)(x-2)<0
=>-8<x<2
h: x^2+4x-21>0
=>(x+7)(x-3)>0
=>x>3 hoặc x<-7
i: x^2-9x-22<0
=>(x-11)(x+2)<0
=>-2<x<11
l: 16x^2+40x+25<0
=>(2x+5)^2<0(loại)
m: 3x^2-4x-4>=0
=>3x^2-6x+2x-4>=0
=>(x-2)(3x+2)>=0
=>x>=2 hoặc x<=-2/3
NH
0
\(7,\) \(a,\left(2x-3y\right)^2-\left(2x+3y\right)^2=\left(3x-2y\right)^2-\left(3x+2y\right)^2\)
\(\Leftrightarrow4x^2-12xy+9y^2-4x^2-12xy-9y^2=9x^2-12xy+4y^2-9x^2-12xy-4y^2\)
\(\Leftrightarrow-24xy=-24xy\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
\(b,\left(a^2+b^2\right)\left(c^2+d^2\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+2acbd+\left(bd\right)^2+\left(ad\right)^2-2adbc+\left(bc\right)^2\)
\(\Leftrightarrow\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2=\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2\) ( luôn đúng )
Vậy 2 đẳng thức ở 2 vế bằng nhau.
*Ở câu \(b,\) dòng thứ 3, vế phải triệt tiêu \(2acbd-2adbc\) \(=0\) nên mất rồi nha.
cảm ơn mn nhiều =^