Bài 53:
Tìm số abcd. Biết abcd + abc + ab + a = 5135
(Cách giải bằng cách sử dụng tính chất PHÉP CHIA CÓ DƯ.)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

abcd +abc+ ab+a = 5135
Sắp xếp lại các chữ số ta có:
aaaa+bbb+cc+d =
1111 x a + (111 x b+11 x c+d) = 5135
Như vậy:
5135 : 1111 = a (dư _ 111 x b+11 x c+d)
5135 : 1111 = 4 (dư 871)
a = 4 và 111 x b+11 x c+d = 871
Tương tự:
871 : 111 = 7 (dư 94)
b = 7 và 11 x c + d = 94
Tương tự:
94 : 11 = 8 (dư 6)
c = 8 và d = 6
Số cần tìm là: 4786

Bài 1:
(abcd) + (abc) + (ab) + (a) = 1111.a + 111.b + 11.c + d
Vậy 1111.a + 111.b + 11.c + d = 4321
+ Nếu a < 3 => 111.b + 11.c + d > 2098 (vô lý vì b, c, d < 10)
+ Nếu a > 3 => vế trái > 4321
Vậy a = 3 => 111.b + 11.c + d = 988
+ Nếu b < 8 => 11.c + d > 210 (vô lý vì c, d < 10)
+ Nếu b > 8 => vế trái > 988
Vậy b = 8 => 11.c + d = 100
+ Nếu c < 9 => d > 11 (vô lý)
Vậy c = 9; d = 1
=> (abcd) = 3891
bài 2:
số tự nhiên A chia cho 29 dư 5 nghĩa là A = 29p + 5 ( p ∈ N ) tương tự A = 31q + 28 ( q ∈ N ) nên
31q + 28 = 29p + 5 ở đây p > q vì nếu p ≤ q ta được 31q - 29 p + 23 = 0 là vô lý vì 31q - 29 p + 23 > 0 với giả thiết p ≤ q ( 29p ≤ 29q < 31q )
vậy p > q ta có 29 ( p - q ) = 23 + 2q vì A là nhỏ nhất nên với p, q ở trên thì p - q nhỏ nhất = 1 thay lại vào ta được q = ( 29 - 23 ) : 2 = 3 vậy p = 4 thay vào ta được A = 29. 4 + 5 = 121
Thử lại 121 = 31 . 3 + 28 thỏa mãn đề bài

Ta thấy c + c = c . Mà số duy nhất cộng nó ra chính nó là 0. Vậy c = 0
c = 0 nên b+c = b là hiển nhiên.
Ta có:a + a = d.
Vì dbc = bcc, nên d = c = b. Vậy, d và b bằng 0 => Vô lý (bạn nên xem lại đề)

abcd +abc+ ab+a = 5135
a x 1000+b x100+ c x 10 + d +a x100 +b x 10 +c +a x10 +b +a = 5315
a x 1111+b x 111+c x11 +d = 5315
Số dư r
Như vậy 5315 : 1111 = a ( dư : b x 111+c x11 +d )
5315 : 1111 = 4 ( dư : 871)
a = 4
Tương tự: 871 = b x 111+c x11 +d
871 : 111 = 7 ( dư : 94)
b = 7
Tương tự: 94 = c x11 +d
94 : 11 = 8 (dư : 6)
C = 8 và d = 6
Vậy so cần tìm: abcd = 4786

1a/
17.4 = 17.(2.2) = (17.2).2 = 34.2 = 68
25.28 = 25.(4.7) = (25.4).7 = 100.7 = 700
b/
13.12 = 13.(10+2) = 13.10 + 13.2
= 130 + 26 = 156
53.11= 53.(10+1) = 53.10 + 53.1
= 530 + 53 = 583
39.101 = 39.(100+1) = 39.100 + 39.1
= 3900 + 39 = 3939
1) a/ 17.4 = 17.2.2 = 34.2 = 68
25.28 = 25.4.7 = 100.7 = 700
b/ 13.12 = 13.10 + 2 = 130 + 2 = 132
53.11 = 53.10 + 1 = 530 + 1 = 531
39.101 = 39.100 + 1 = 3900 + 1 = 3901
2) 8.19 = 8. ( 20 - 1 )
= 8.20 - 8.1
= 160 - 8 = 152
65.98 = 65. ( 100 - 2 )
= 65.100 - 65.2
= 6500 - 130 = 6370
3) - STN nhỏ nhất có 3 chữ số khác nhau là: 102
- STN lớn nhất có 3 chữ số khác nhau là: 987
Tổng của STN nhỏ nhất có 3 chữ số khác nhau và STN lớn nhất có 3 chữ số khác nhau là:
987 + 102 = 1098
Đ/S: 1098
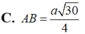
abcd + abc + ab + a = 5135
a x 1000 + b x 100 + c x 10 + d + a x 100 + b x 10 + c + a x 10 + b + a = 5135
a x 1111 + b x 111 + c x 11 + d = 5135
Vậy : a = 4 ; b = 6 ; c = 2 ; d = 3
abcd +abc+ ab+a = 5135
Sắp xếp lại các chữ số ta có:
aaaa+bbb+cc+d =
1111 x a + (111 x b+11 x c+d) = 5135
Như vậy:
5135 : 1111 = a (dư _ 111 x b+11 x c+d)
5135 : 1111 = 4 (dư 871)
a = 4 và 111 x b+11 x c+d = 871
Tương tự:
871 : 111 = 7 (dư 94)
b = 7 và 11 x c + d = 94
Tương tự:
94 : 11 = 8 (dư 6)
c = 8 và d = 6
Số cần tìm là: 4786
Các bạn có thấy đúng không nếu đúng các bạn k cho tớ để tớ làm vào vở cho chắc ăn