dung cosi nha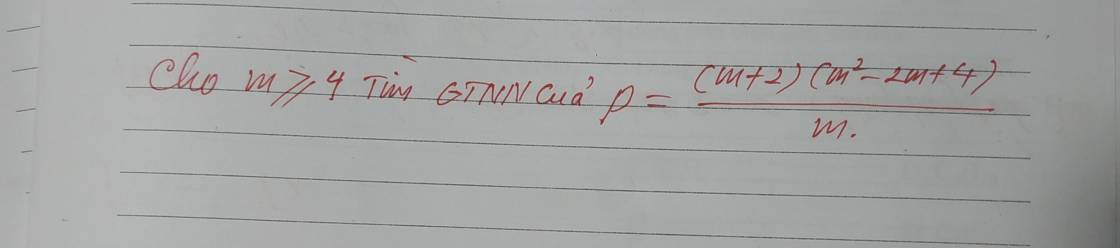 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
0
10 tháng 8 2019
ĐK: \(0\le x\le1\)
\(VT=\sqrt{x\left(x+1\right)}+\sqrt{x\left(1-x\right)}\le\frac{x+x+1+x+1-x}{2}=\frac{2x+2}{2}=x+1\)
Dấu "=" ko xảy ra
NC
1
DH
8 tháng 12 2019
Cosi là một bất đẳng thức.
1 Số các kiến thức cơ bản nè:
* Chuyển từ tổng sang tích và tích sang tổng
\(a+b\ge2\sqrt{ab}\Leftrightarrow\sqrt{ab}\le\frac{a+b}{2}\) ( a+b là 2 số thì bên kia là a.b và do có 2 số nên nó là căn bậc 2 và có số 2 đằng trước).
Thêm 1 cái nữa cho dễ nhìn nha:
\(a+b+c+d\ge4\sqrt[4]{abcd}\Leftrightarrow\sqrt[4]{abcd}\le\frac{a+b+c+d}{4}\)
20 tháng 8 2021
Nói thật với bạn mình không biết sử dụng BĐT Cô si cho dạng này, nhưng mình có một cách làm dễ hơn, bạn tham khảo nhé.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 8 2021
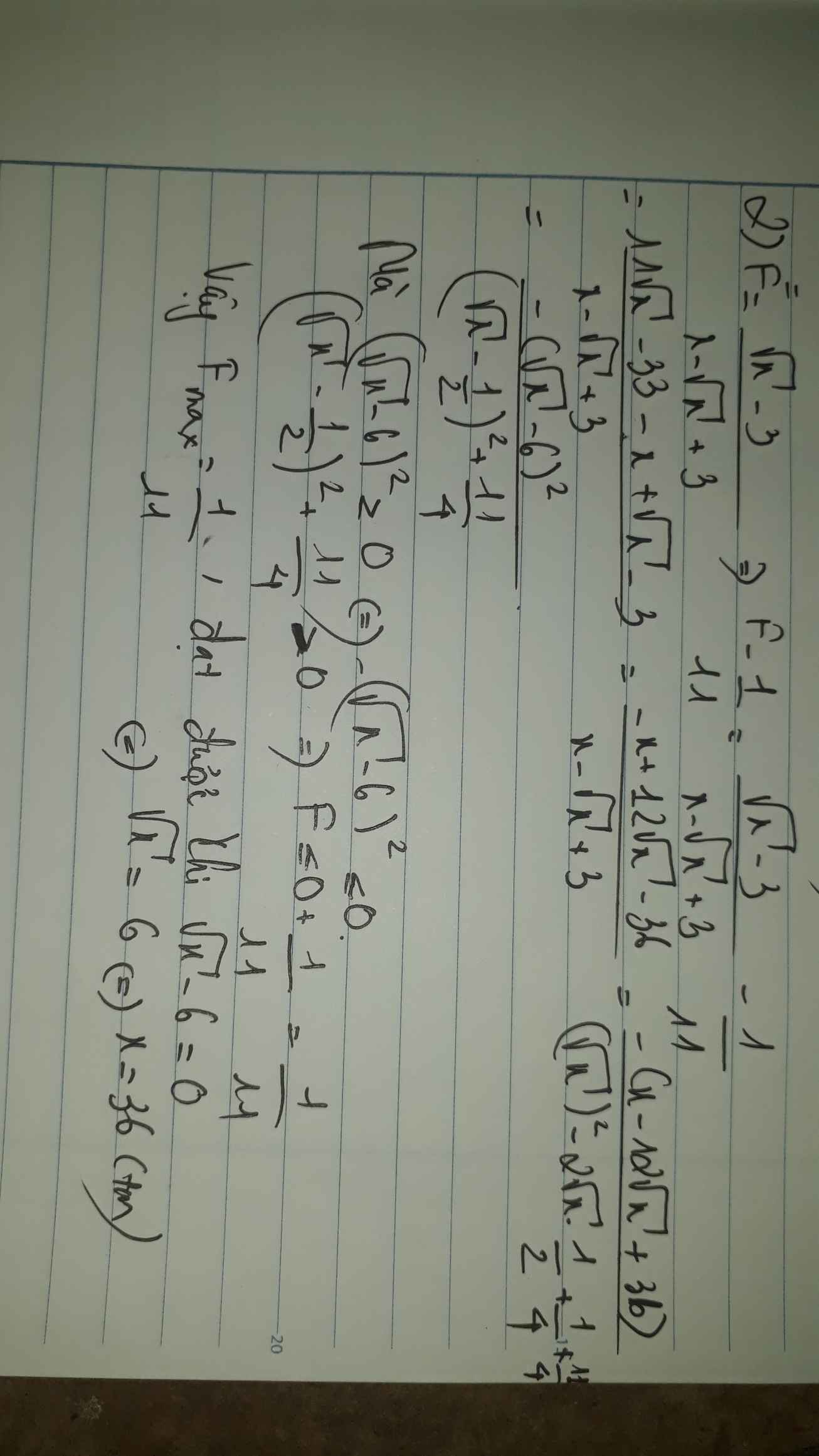
\(x>9\Rightarrow\sqrt{x}-3>0\Rightarrow F>0\)
\(\dfrac{1}{F}=\dfrac{x-\sqrt{x}+3}{\sqrt{x}-3}=\sqrt{x}+2+\dfrac{9}{\sqrt{x}-3}=\sqrt{x}-3+\dfrac{9}{\sqrt{x}-3}+5\ge2\sqrt{\dfrac{9\left(\sqrt{x}-3\right)}{\sqrt{x}-3}}+5=11\)
\(\Rightarrow F\le\dfrac{1}{11}\)
\(F_{max}=\dfrac{1}{11}\) khi \(\sqrt{x}-3=3\Rightarrow x=36\)
13 tháng 9 2021
c) Ta có: \(C=\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}=\sqrt{x}+\dfrac{1}{\sqrt{x}+1}=\left(\sqrt{x}+1\right)+\dfrac{1}{\sqrt{x}+1}-1\)
Áp dụng BĐT Cô-si ta có:
\(\sqrt{x}+1+\dfrac{1}{\sqrt{x}+1}\ge2\sqrt{\left(\sqrt{x}+1\right).\dfrac{1}{\sqrt{x}+1}}=2\)
\(\Rightarrow C\ge2-1=1\)
Dấu "=" xảy ra ⇔ \(\sqrt{x}+1=1\Leftrightarrow x=0\)
13 tháng 9 2021
a)
Ta có: \(A=\sqrt{x}-1+\dfrac{4}{\sqrt{x}-1}\ge2\sqrt{\left(\sqrt{x}-1\right).\dfrac{4}{\sqrt{x}-1}}=2\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\sqrt{x}-1\right)^2=4\Leftrightarrow\sqrt{x}-1=2\Leftrightarrow x=9\)
15 tháng 3 2020
Áp BĐT Cô-si
1. Cho a,b,c ≥≥ 0. Chứng minh các BĐT sau
a. (1+a)(1+b)(1+c)≥(1+3√abc)3(1+a)(1+b)(1+c)≥(1+abc3)3
b. a2(1+b2)+b2(1+c2)+c2(1+a2)≥6abca2(1+b2)+b2(1+c2)+c2(1+a2)≥6abc
c. aba+b+bcb+c+cc+a≤a+b+c2aba+b+bcb+c+cc+a≤a+b+c2
d. ab+c+bc+a+ca+b≥32
`P=((m+2)(m^2-2m+4))/m`
`=(m^3+8)/m`
`=m^2+8/m`
`=(m^2+64/m+64/m)-120/m`
Theo BĐT côsi cho ba số dương `m^2;64/m;64/m` ta có:
`m^2+64/m+64/m >= 3\root[3]{m^2 . 64/m . 64/m}=48(1)`
Mặt khác: `m>=4` nên `120/m<=30 =>-120/m>=-30(2)`
Cộng hai vế của `(1)` và `(2)` có `P>=48-30=18`
Dấu "=" xảy ra `<=>{(m^2=64/m),(m=4):}<=>m=4`
Vậy `P_(min)=18<=>m=4`