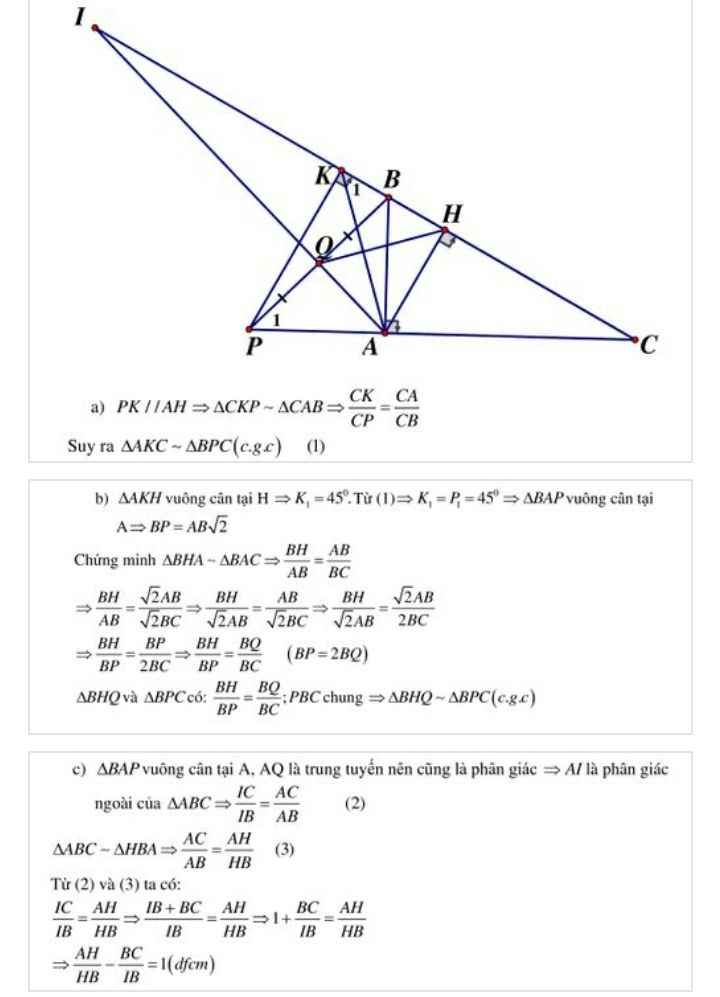
Cho tam giác ABC vuông tại A (AC>AB). Vẽ đường cao AH . Trên tia đối của tia BC lấy điểm K sao cho KH=HA. Qua K kẻ đường thẳng song song với AH cắt AC tại P
a) Chứng minh: Tam giác ABC đồng dạng với tam giác KPC
b) Gọi Q là trung điểm của BP. Chứng minh: QH là đường trung trực của đoạn thẳng AK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

19 tháng 10 2020
a) 2 tâm giác vuông có 1 góc nhọn bằng nhau
b) QK=QA suy ra dpcm

10 tháng 1
Xét tứ giác ABDC có
AB//DC
AC//BD
Do đó: ABDC là hình bình hành
=>AD cắt BC tại trung điểm của mỗi đường
=>K là trung điểm chung của AD và BC
Xét ΔAED có
H,K lần lượt là trung điểm của AE,AD
=>HK là đường trung bình của ΔAED
=>HK//ED
Ta có: HK//ED
HK\(\perp\)AE
Do đó: ED\(\perp\)AE
=>ΔAED vuông tại E
Ta có: ΔEAD vuông tại E
mà EK là đường trung tuyến
nên KE=KD
=>ΔKED cân tại K