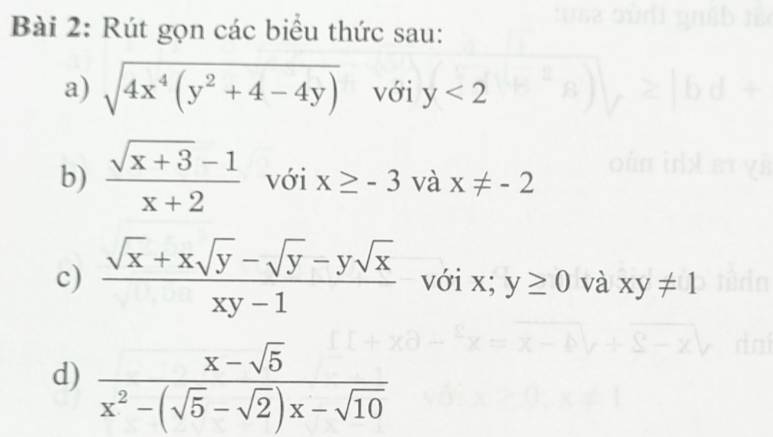ai giúp mình được không ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
Đỗ Thanh Hải
CTVVIP
7 tháng 8 2021
1 Although
2 Although
3 however
4 Despite
5 Nevertheless
6 Despite
7 However
8 in spite
9 Although
10 Despite
11 in spite of
12 Despite
13 Although
14 despite
ai giúp mình được không ạ
30 tháng 5 2023
c: A^2=2004+2006+2*căn 2005^2-1=4010+2*căn 2005^2-1
B^2=(2căn2005)^2=4010+2*căn 2005^2
=>A^2<B^2
=>A<B
d: \(A=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}+1-\sqrt{7}+1-2\right)=0\)
2 tháng 7 2023
d: Xét ΔBKM và ΔAKC có
góc KBM=góc KAC
KB=KA
góc BKM=góc AKC
=>ΔBKM=ΔAKC
Xét ΔABC có
AH,CK là trung tuyến
AH cắt CK tại G
=>G là trọng tâm
=>CG=2/3CK
=>2CK=3CG=CM
AC+BC=BM+BC>CM=3CG
TT
0
A
1
13 tháng 10 2021
Bài 10:
a: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-8=-2x-3\\y=3x-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-8=-5\end{matrix}\right.\)
Thay x=1 và y=-5 vào (d3), ta được:
\(3m+2m+1=-5\)
hay \(m=-\dfrac{6}{5}\)
M
1
26 tháng 1 2023
a: \(=\dfrac{2x+x-2-x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2}{x+2}\)
b: x^2-x-6=0
=>(x-3)(x+2)=0
=>x=3(nhận) hoặc x=-2(loại)
Khi x=3 thì \(E=\dfrac{2}{3+2}=\dfrac{2}{5}\)
c: Để E nguyên thì \(x+2\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{-1;-3;0;-4\right\}\)
18 tháng 9 2021
tùy bạn thôi có nhiều kiểu vẽ tay khác nhau lắm, khó thì vẽ tay hình tròn bánh bao, dễ lắm =))
18 tháng 9 2021
vậy á, mình không có học vẽ, mình vẽ chơi chơi rảnh thì lên mạng xem vẽ thôi tầm được có 5 năm à
a.
\(=\sqrt{\left(2x^2\right)^2}.\sqrt{\left(y-2\right)^2}=2x^2.\left(2-y\right)\)
b.
\(=\dfrac{\sqrt{x+3}-1}{x+3-1}=\dfrac{\left(\sqrt{x+3}-1\right)\left(\sqrt{x+3}+1\right)}{\left(x+3-1\right)\left(\sqrt{x+3}+1\right)}=\dfrac{1}{\sqrt{x+3}+1}\)
c.
\(=\dfrac{\sqrt{x}\left(1+\sqrt{xy}\right)-\sqrt{y}\left(1+\sqrt{xy}\right)}{xy-1}=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(1+\sqrt{xy}\right)}{\left(\sqrt{xy}-1\right)\left(\sqrt{xy}+1\right)}=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{xy}-1}\)
d.
\(=\dfrac{x-\sqrt{5}}{x\left(x+\sqrt{2}\right)-\sqrt{5}\left(x+\sqrt{2}\right)}=\dfrac{x-\sqrt{5}}{\left(x+\sqrt{2}\right)\left(x-\sqrt{5}\right)}=\dfrac{1}{x+\sqrt{2}}\)