một đoạn mạch có điện trở r để giảm bớt điện trở của đoạn mạch đi một lượng bằng R chia 5 phải mắc thêm một phải mắc thêm Cho đoạn mạch một điện trở bao nhiêu và mắc thế nào
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(R=R1+R2=10+5=15\Omega\)
\(I=I1=I2=U:R=12:15=0,8A\left(R1ntR2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}U1=R1.I1=10.8=8V\\U2=R2.I2=5.0,8=4V\end{matrix}\right.\)
\(\left\{{}\begin{matrix}P1=U1.I1=8.0,8=6,4\\P2=U2.I2=4.0,8=3,2\end{matrix}\right.\)W
\(Q_{toa}=UIt=12.15.20.60=216000J\)

Do R1ntR2
\(\Rightarrow\dfrac{U_1}{U_2}=\dfrac{R_1}{R_2}\Rightarrow\dfrac{3}{U_2}=\dfrac{R_1}{1,5R_1}=\dfrac{1}{1,5}\Rightarrow U_2=4,5\left(V\right)\)
\(U=U_1+U_2=3+4,5=7,5\left(V\right)\)
Bài 2:
\(I=\dfrac{U}{R}=\dfrac{3}{12}=0,25\left(A\right)\)

Đáp án D
Để cường độ dòng điện giảm đi còn một nửa thì điện trở của mạch phải tăng lên gấp đôi, vậy R 4 = R 1 + R 2 + R 3 = 60 Ω .

Lúc đầu:\(I=\dfrac{U}{2R}\)
lúc sau:\(I'=\dfrac{U}{3R}\)
Lập tỉ lệ giữa I và I'
\(\dfrac{I}{I'}=\dfrac{\dfrac{U}{2R}}{\dfrac{U}{3R}}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}=\dfrac{3}{2}\Rightarrow\dfrac{I}{I'}=\dfrac{3}{2}\Leftrightarrow\dfrac{3}{I'}=\dfrac{3}{2}\Rightarrow I'=2\left(A\right)\)
vậy ...
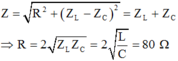

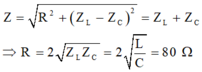
Do đoạn mạch bị giảm điện trở nên ta cần mắc thêm điện trở \(R_1\) song song với đoạn mạch ban đầu. Điện trở tương đương khi mắc thêm điện trở \(R_1\) là \(\dfrac{4R}{5}\)
Ta có: \(R_{tđ}=\dfrac{RR_1}{R+R_1}=\dfrac{4R}{5}\)
\(\Rightarrow\dfrac{R_1}{R+R_1}=\dfrac{4}{5}\)
\(\Rightarrow5R_1=4\left(R+R_1\right)\)
\(\Rightarrow5R_1=4R+4R_1\)
\(\Rightarrow R_1=4R\)
Vậy cần mắc song song với đoạn mạch ban đầu có \(R_1=4R\)
4R/5 ở đau thế ạ