Toán iq á mọi người.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Mỗi lần di chuyển, quân cờ chỉ có thể di chuyển một trong bốn cách sau: lên trên 1 ô (U), xuống dưới 1 ô (D), sang phải 1 ô (R), sang trái 1 ô (L). Quân cờ di chuyển bốn lần sẽ có 4 4 = 256 cách.
⇒ n ( Ω ) = 256 cách
Gọi A là biến cố quân cờ không trở về đúng vị trí ban đầu sau bốn lần di chuyển.
=> A ¯ là biến cố quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển.
Để quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển thì phải thực hiện 1 trong 3 trường hợp sau:
Trường hợp 1: Có một U, một D, một R, một L.
Xếp cách thực hiện U, D, R, L theo thứ tự có 4! = 24 cách.
Trường hợp 2: Có hai U, hai D.
Xếp cách thực hiện hai U, hai D theo thứ tự có ![]() cách.
cách.
Trường hợp 3: Có hai R, hai L.
Xếp cách thực hiện hai R, hai L theo thứ tự có ![]() cách.
cách.
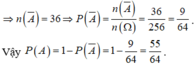

Theo hình ta thấy quãng đường quân hậu di chuyển là 1 tam giác vuông cân có cạnh góc vuông là cạnh chung với cạnh của bàn cờ
Ta có cạnh bàn cờ là \(\sqrt{40}=2\sqrt{10}\left(cm\right)\)
Áp dụng PTG, cạnh huyền của tam giác vuông cân là \(\sqrt{\left(2\sqrt{10}\right)^2+\left(2\sqrt{10}\right)^2}=4\sqrt{10}\left(cm\right)\)
Vậy tổng quãng đường quân hậu di chuyển là \(2\sqrt{10}\cdot2+4\sqrt{10}=8\sqrt{10}\left(cm\right)\)

Một bàn cờ vua tiêu chuẩn sẽ có 8*8=64 ô.
Trừ ô quân Mã đứng, còn lại 63 ô.
Như vậy vì quân Mã di chuyển qua tất cả các ô, mỗi ô chỉ được đi qua 1 lần nên quân Mã sẽ phải thực hiện 63 nước đi.
Đặc điểm của quân Mã là nếu đi số nước lẻ thì nó sẽ dừng lại ở ô khác màu với ô nó đứng ban đầu, mà 63 là số lẻ do đó nơi nó kết thúc trong hành trình này sẽ là một ô khác màu với ô ban đầu nó đứng.
Nhưng góc đối diện với ô quân Mã đứng lúc đầu lại là ô cùng màu (vì nằm trên cùng đường chéo) nên việc quân Mã kết thúc tại góc đối diện theo đề bài sẽ không bao giờ có thể xảy ra.
Vậy không thể di chuyển Mã như đề bài yêu cầu.

Gọi tổng số hạt thóc là A thì ta có phép tính:
\(A=1+2+2^2+2^3+...+2^{31}\)
\(\Rightarrow2A=2+2^2+2^3+2^4...+2^{32}\)
\(\Rightarrow2A-A=\left(2+2^2+2^3+2^4...+2^{32}\right)-\left(1+2+2^2+2^3+...+2^{31}\right)\)
\(\Rightarrow A=2^{32}-1\)
\(\Rightarrow A=\text{4 294 967 296}-1=\text{4 294 967 295}\)
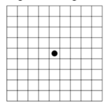
Ta đánh dấu bảng 5x5 như trên và không mất tính tổng quát, giả sử quân mã ban đầu ở vị trí a1. Khi đó một đường đi của quân mã để đi hết tất cả các ô trên bàn cờ (với điều kiện mỗi ô chỉ được đi qua 1 lần) là:
a1-c2-e1-d3-e5-c4-a5-b3-c1-e2-d4-b5-a3-b1-d2-e4-c5-a4-b2-d1-e3-d5-b4-a2-c3.
cái này đúng rồi á chị nhưng mà nhìn bàn cờ nó cũng cứ kiểu gì ấy....
Hì hì...