giú mk câu b với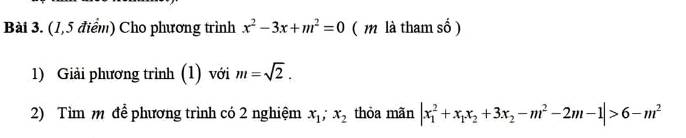
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số ghế băng dài lúc đầu trong phòng họp là x(cái)
thì số ghế băng dài lúc sau trong phòng hợp là x+6(cái)
Số người ngồi trong 1 ghế băng dài lúc đầu là y(người)
Số người ngồi trong 1 ghế băng dài lúc sau là y-1(người)
Đk x,y∈N*
Theo đề bài ta có
\(\left\{{}\begin{matrix}xy=36\\\left(x+6\right)\left(y-1\right)=36\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}xy=36\\xy-x+6y-6=36\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}xy=36\\36-x+6y-6=36\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}xy=36\\-x+6y=6\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=\dfrac{36}{x}\\-x+6\cdot\dfrac{36}{x}=6\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=\dfrac{36}{x}\\-x^2-6x+216=0\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=\dfrac{36}{x}\\\left(x-12\right)\left(x+18\right)=0\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=\dfrac{36}{x}\\\left[{}\begin{matrix}x-12=0\\x+18=0\end{matrix}\right.\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}y=\dfrac{36}{x}\\\left[{}\begin{matrix}x=12\left(N\right)\\x=-18\left(l\right)\end{matrix}\right.\end{matrix}\right.\)
⇒x=12
Vậy......

Bạn ơi đáng phải là 6y-7 chứ bạn bài này cô mk vừa dạy hôm qua
Vì x,y nguyên và ( 2x-5 ).( 6y-7 ) = 13
Ta có bảng :
| 2x-5 | 1 | 13 | -1 | -13 |
| 6y-7 | 13 | 1 | -13 | -1 |
| x | 3 | 9 | 2 | -4 |
| y | L | L | -1 | 1 |

1 C
2 B
3 C
4 D
5 A
6 good for
7 who
8 students
9 would tell
10 to smoke
11 latest

\(A=\frac{4}{n-2}+\frac{6}{n-2}-\frac{3}{n-2}\)
\(A=\frac{4+6-3}{n-2}=\frac{7}{n-2}\)
nấu bạn muốn tìm n sao cho A nguyên thì \(7⋮n-2\)
\(n-2\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
do đó \(n\in\left\{3;1;9;-5\right\}\)
HT

Chắc đề bài là xét tính liên tục của hàm số?
e.
\(\lim\limits_{x\rightarrow5}f\left(x\right)=\lim\limits_{x\rightarrow5}\dfrac{\sqrt[]{4x+16}+4-2x}{x^2-5x}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(\sqrt[]{4x+16}-6\right)+10-2x}{x^2-5x}=\lim\limits_{x\rightarrow5}\dfrac{\dfrac{\left(\sqrt[]{4x+16}-6\right)\left(\sqrt[]{4x+16}+6\right)}{\sqrt[]{4x+16}+6}-2\left(x-5\right)}{x\left(x-5\right)}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\dfrac{4\left(x-5\right)}{\sqrt[]{4x+16}+6}-2\left(x-5\right)}{x\left(x-5\right)}=\lim\limits_{x\rightarrow5}\dfrac{\dfrac{4}{\sqrt[]{4x+16}+6}-2}{x}\)
\(=\dfrac{\dfrac{4}{\sqrt[]{4.5+16}+6}-2}{5}=-\dfrac{1}{3}\)
\(f\left(5\right)=-\dfrac{1}{3}\)
\(\Rightarrow\lim\limits_{x\rightarrow5}f\left(x\right)=f\left(5\right)\)
Hàm liên tục tại \(x_0=5\)
f.
\(\lim\limits_{x\rightarrow-1}f\left(x\right)=\lim\limits_{x\rightarrow-1}\dfrac{x^3+x+2}{x^3+1}\)
\(=\lim\limits_{x\rightarrow-1}\dfrac{\left(x+1\right)\left(x^2-x+2\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\lim\limits_{x\rightarrow-1}\dfrac{x^2-x+2}{x^2-x+1}\)
\(=\dfrac{1+1+2}{1+1+1}=\dfrac{4}{3}\)
Và \(f\left(-1\right)=\dfrac{4}{3}\)
\(\Rightarrow\lim\limits_{x\rightarrow-1}f\left(x\right)=f\left(-1\right)\)
Hàm liên tục tại \(x_0=-1\)

Được thôi ,và mik cx là người mới mong chúng mik cùng giúp đỡ nhauありがと

Trường hợp 1: m=0
Bất phương trình sẽ trở thành -3<0(luôn đúng)
Trường hợp 2: m<>0
\(\text{Δ}=\left(2m\right)^2-4\cdot m\cdot\left(-3\right)=4m^2+12m\)
Để bất phương trình có nghiệm đúng với mọi x thì \(\left\{{}\begin{matrix}4m\left(m+3\right)< 0\\m< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3< m< 0\\m< 0\end{matrix}\right.\Leftrightarrow-3< m< 0\)
Vậy: -3<m<=0

Dễ thấy hiển nhiên số cần tìm là số có hai chữ số.
Gọi số đó là \(\overline{ab}\).
Khi đó: \(\overline{ab}+2\left(a+b\right)=10a+b+2a+2b=12a+3b=93\Leftrightarrow4a+b=31\)
\(0\le b\le9\Rightarrow22\le4a\le31\Rightarrow a\in\left\{6,7\right\}\)
Suy ra các số thỏa mãn là: \(67,73\).




Lời giải:
Theo định lý Viet:
$x_1+x_2=3$
$x_1x_2=m^2$
Khi đó:
$|x_1^2+x_1x_2+3x_2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |x_1^2+x_1x_2+(x_1+x_2)x_2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |x_1^2+2x_1x_2+x_2^2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |(x_1+x_2)^2-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |9-m^2-2m-1|> 6-m^2$
$\Leftrightarrow |m^2+2m-8|> 6-m^2$
Nếu $m^2+2m-8\geq 0$ thì:
$m^2+2m-8> 6-m^2$
$\Leftrightarrow 2m^2+2m-14>0$
$\Leftrightarrow m^2+m-7>0$
$\Leftrightarrow m< \frac{-1-\sqrt{29}}{2}$ hoặc $m> \frac{-1+\sqrt{29}}{2}$
Kết hợp với $m^2+2m-8\geq 0$ suy ra $m\leq -4$ hoặc $m> \frac{-1+\sqrt{29}}{2}$
Nếu $m^2+2m-8<0$ thì:
$-(m^2+2m-8)> 6-m^2$
$\Leftrightarrow m< 1$
Kết hợp với $m^2+2m-8<0$ suy ra $-4< m< 1$
Vậy........