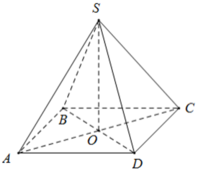
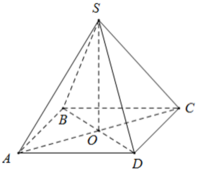
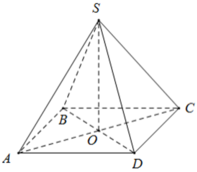
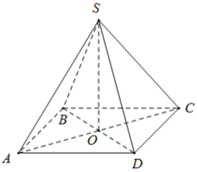
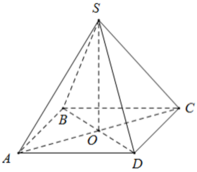
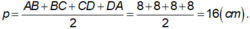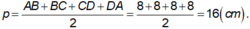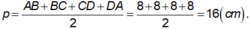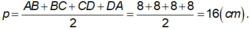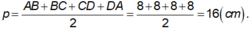Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy = 12cm , cạnh bên = 10cm
a, Tính diện tích toàn phần của S,ABCD
b, Tính thể tích của S,ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 1 2017
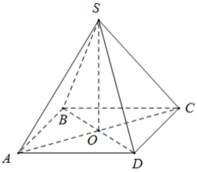
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
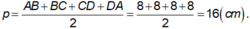
+ BD = AC = √ (82 + 82) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )
Do đó:
+ Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm2 ).
+ Diện tích toàn phần của hình chóp đều là
Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 ( cm2 )
+ Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3( cm3 )
18 tháng 8 2023
a: Gọi O là tâm của hình vuông ABCD
S.ABCD là tứ giác đều có O là tâm của đáy ABCD
=>SO là trung đoạn và SO vuông góc (ABCD)
ABCD là hình vuông
=>\(AC=BD=\sqrt{12^2+12^2}=12\sqrt{2}\left(cm\right)\)
=>\(OA=OB=OC=OD=6\sqrt{2}\left(cm\right)\)
ΔSOA vuông tại O
=>SO^2+OA^2=SA^2
=>\(SO^2=10^2-\left(6\sqrt{2}\right)^2=100-72=28\)
=>\(SO=2\sqrt{7}\left(cm\right)\)
b: \(S_{xq}=\dfrac{C_{đáy}}{2}\cdot SO\)
\(=2\sqrt{7}\cdot\left(12\cdot\dfrac{4}{2}\right)=2\sqrt{7}\cdot24=48\sqrt{7}\left(cm^2\right)\)
\(S_{tp}=48\sqrt{7}+12^2=48\sqrt{7}+144\left(cm^2\right)\)
H
18 tháng 8 2023
a.
Độ dài trung đoạn của hình chóp là:
\(\sqrt{12^2-10^2}=2\sqrt{11}\left(cm\right)\)
b.
Diện tích xung quanh của hình chóp là:
\(S_{xq}=\dfrac{8.4}{2}.2\sqrt{11}.\dfrac{1}{2}=16\sqrt{11}\left(cm^2\right)\)
Diện tích toàn phần của hình chóp là:
\(S_{tp}=16\sqrt{11}+12^2=197\left(cm^2\right)\)
CM
7 tháng 8 2019
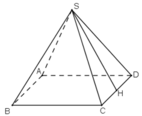
Gọi H là trung điểm của CD
Vì ΔSCD cân tại S, có SH là đường trung tuyến nên đồng thời là đường cao
⇒ SH ⊥ CD.
Ta có:
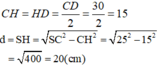
Chu vi đáy là: 4. 30 = 120 (cm)
Diện tích xung quanh của hình chóp:
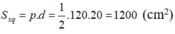
Diện tích đáy: Sd = 302 = 900 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sd = 1200 + 900 = 2100 (cm2)