Câu 8: Cho đường tròn tâm O đường kính AB . Kẻ dây cung CD vuông góc với AB tại H (H nằm giữa A và 0,H khác A và O). Lấy điểm G thuộc CH (G khác C và H),tia AG cắt đường tròn tại E khác A. Gọi K là giao điểm của hai đường thẳng BE và CD a) Chứng minh tứ giác BEGH là tứ giác nội tiếp và KC. KD = KEKB
b) Đoạn thẳng AK cắt đường tròn O tại F khác 4. Chứng minh G là tâm đường tròn nội tiếp tam giác HEF.
c) Gọi M, N lần lượt là hình chiếu vuông góc của A và B lên đường thẳng EF. Chứng minh (HE + HF)/(MN) = 1

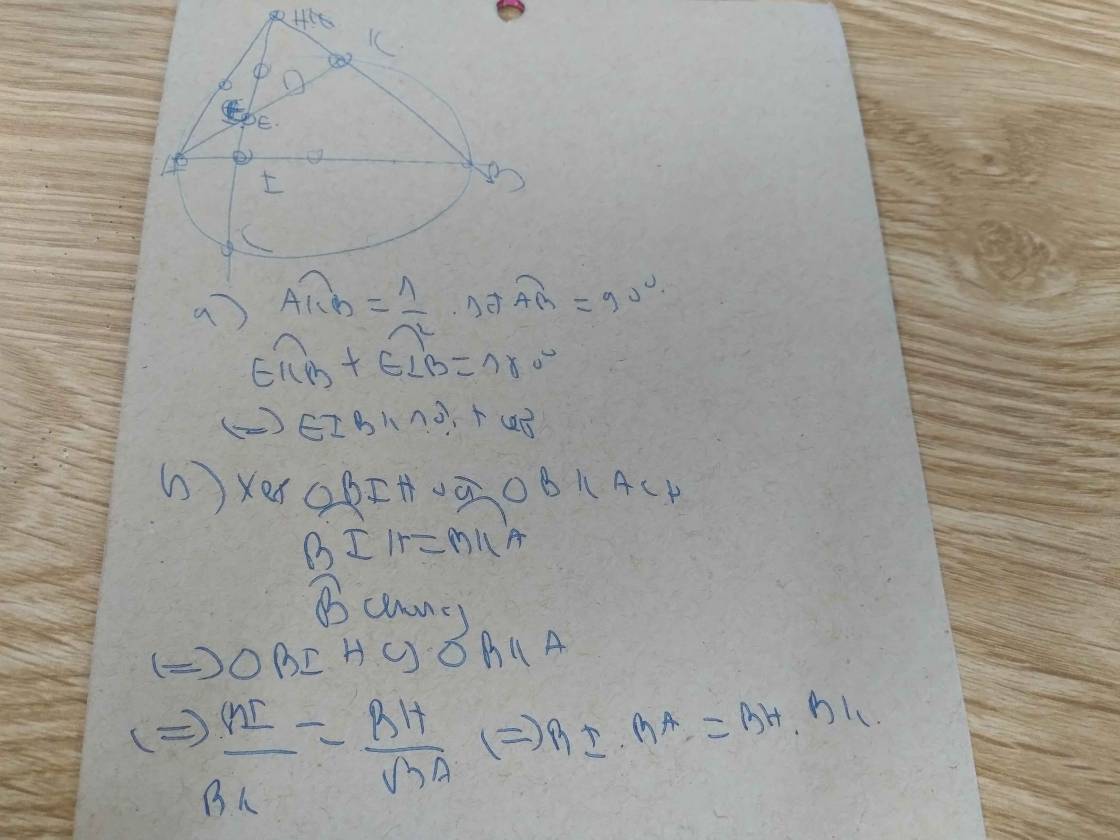

a: góc AEB=góc AFB=90 độ
góc GHB+góc GEB=180 độ
=>GHBE nội tiếp
b: góc AFG+góc AHG=180 độ
=>AFGH nội tiếp
góc FEG=góc AKH
góc HEG=góc FBA
góc AKH=góc FBA
=>góc FEG=góc HEG
=>EG là phân giác của goc FEH
góc EFG=góc HKB
góc HFG=góc EAB
góc HKB=góc EAB
=>góc EFG=góc HFG
=>FG là phân giác của góc HFE
=>G là tâm đường tròn nội tiếp ΔFEH