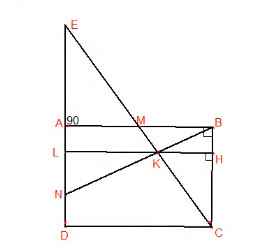
Cho hình vuông ABCD cạnh 12 cm.M là trung điểm cạnh BC.Đoạn thẳng AM và đoạn thẳng BN cắt nhau tại O. N là trung điểm của DC
a/.Tính chu vi và diện tích hình vuông
b/. Chứng tỏ diện tich hình tam giác ABN gấp 4 lần diện tích tam giác BMN
c/. Tính diện tích tứ giác AOND

a ) Chu vi hình vuông ABCD là :
12 x 4 = 48 ( cm )
Diện tích hình vuông ABCD là :
12 x 12 = 144 ( cm2 )
b ) Diện tích tam giác ABN bằng 1/2 diện tích hình vuông , vậy diện tích tam giác ABN là :
144 : 2 = 72 ( cm2 )
Tam giác BMN có đáy BM = 1/2 BC = 12 : 2 = 6 ( cm )
Và đường cao tương ứng là đoạn NC = 1/2 CD = 12 : 2 = 6 ( cm )
Diện tích tam giác BMN bằng :
6 x 6 : 2 = 18 ( cm2 )
Vì 72/18 = 4 nên diện tích tam giác ABN gấp 4 lần diện tích tam giác BMN .
c) dt AMN = dt ABCD - ( dt ABM + dt MCN + dt ADN )
= 144 - ( 36 + 18 + 36 )
= 54 cm2 .
Hai tam giác ABN và BMN có cùng đáy NB mà dt ABN gấp 4 lần dt BMN nên đường cao hạ từ đỉnh A gấp 4 lần đường cao hạ từ đỉnh M .
Xét hai tam giác AON và MON có cùng đáy NO và đường cao hạ từ đỉnh A gấp 4 lần đường cao hạ từ đỉnh M nên dt tam giác AON gấp 4 lần dt tam giác MON .
Vậy dt tam giác AON là :
54 : ( 4 + 1 ) x 4 = 43,2 ( cm2 )
dt tứ giác AOND = dt tam giác AON + dt tam giác AND .
= 43 ,2 + 36
dt tứ giác AOND = 79,2 ( cm2 )
CAU CO PHAI LA LAN B KHONG