1. cho Parabol (P): y= -1/2x2 và đường thẳng (D): y= 1/2x-1
a) vẽ (P) và (D) trên cùng một mặt phẳng tọa độ.
b) tìm tọa dộ giao điểm của (P) vad (D) bằng phép toán.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chào ng đẹp
a) tự vẽ
b) pt hoành độ 1/2x^2=3/2x-1
Giải pt bậc 2 ra có x1=..;x2=..
thay lần lượt x1=...;x2=.... vô y=1/2x^2
ta dc y1=..;y2=...
ta được 2 giao điểm của (P) và (d) là A(x1;y1);B(x2;y2)
a,y=1/2x2
bạn lập bảng giá trị :
| x | -2 | -1 | 0 | 1 | 2 |
| y | 2 | 1/2 | 0 | 1/2 | 2 |
sau đó thay vào vẽ parabol .
b,vì là giao điểm của (P) và (d) nên suy ra :
\(\frac{1}{2}\)x2= \(\frac{3}{2}\)x-1
chuyển thành pt bậc 2 và giải ta đk kết quả của x là hoành độ , y là tung độ của giao điểm
chúc bạn học tập tốt phần này vì nó là kiến thức quan trọng cho th vào lớp 10

a: 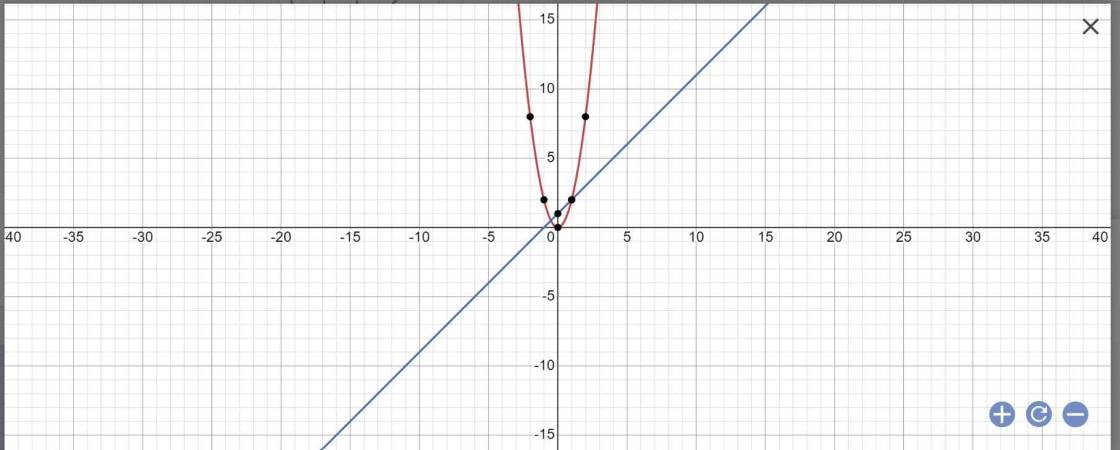
b: PTHĐGĐ là:
2x^2=x+1
=>2x^2-x-1=0
=>2x^2-2x+x-1=0
=>(X-1)(2x+1)=0
=>x=-1/2 hoặc x=1
=>y=2*1/4=1/2 hoặc y=2

a)
\(\left(P\right):y=x^2\)
Ta có bảng
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Vậy đồ thị hàm số \(y=x^2\) là một parabol lần lượt đi qua các điểm
\(\left(-2;4\right),\left(-1;1\right),\left(0;0\right),\left(1;1\right),\left(2;4\right)\)
Bạn tự vẽ nhé
\(\left(d\right):y=-2x+3\)
Cho \(y=0\Rightarrow x=\dfrac{3}{2}\Rightarrow A\left(\dfrac{3}{2};0\right)\in Ox\)
Cho \(x=0\Rightarrow y=3\Rightarrow B\left(0;3\right)\in Oy\)
Vẽ đường thẳng AB ta được đths \(y=-2x+3\)
Bạn tự bổ sung vào hình vẽ nhé
b) Xét PTHĐGĐ của \(\left(P\right),\left(d\right)\) là nghiệm của phương trình
\(x^2=-2x+3\\ \Leftrightarrow x^2+2x-3=0\)
Xét \(a+b+c=1+2-3=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với `x=1 => y=x^2 = 1`
Với `x=2 => y=x^2 = 4`
Vậy tọa độ giao điểm của \(\left(P\right),\left(d\right)\) là 2 điểm \(\left(1;1\right)\) và \(\left(2;4\right)\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2+x-2=0\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(x-1\right)=0\\y=-x+2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;4\right);\left(1;1\right)\right\}\)

a: 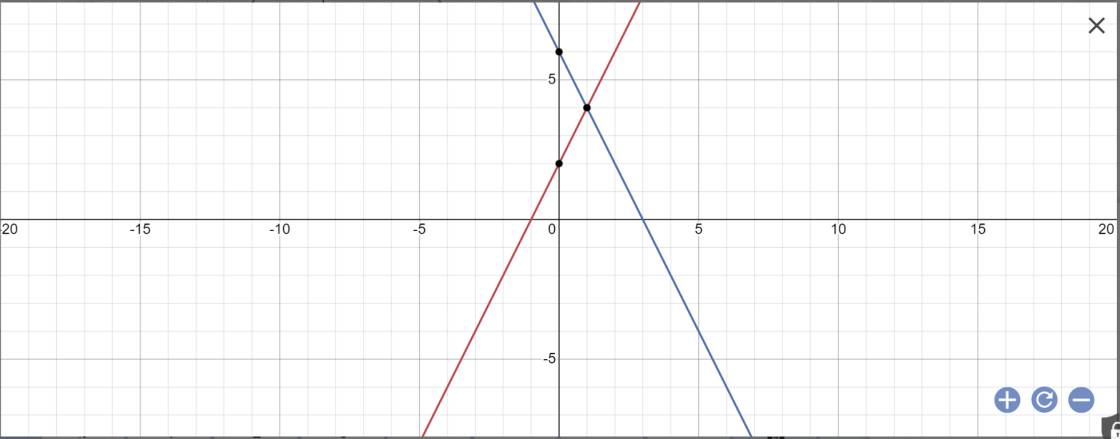
b: Phương trình hoành độ giao điểm là:
2x+2=6-2x
=>2x+2x=6-2
=>4x=4
=>x=1
Thay x=1 vào y=2x+2, ta được:
\(y=2\cdot1+2=4\)
Vậy: (d1) cắt (d2) tại A(1;4)
c: Thay x=0 vào y=x-6, ta được:
y=0-6=-6
Thay x=0 và y=-6 vào y=ax+b, ta được:
\(a\cdot0+b=-6\)
=>b=-6
=>y=ax-6
Thay x=2 vào y=2x+1, ta được:
\(y=2\cdot2+1=5\)
Thay x=2 và y=5 vào y=ax-6, ta được:
2a-6=5
=>2a=11
=>\(a=\dfrac{11}{2}\)

c: Vì (d2)//(d) nên \(a=-\dfrac{1}{2}\)
Thay x=-3 và y=0 vào \(y=\dfrac{-1}{2}x+b\), ta được:
\(b+\dfrac{3}{2}=0\)
hay \(b=-\dfrac{3}{2}\)

b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x^2=-\dfrac{1}{2}x-1\)
\(\Leftrightarrow-\dfrac{1}{2}x^2+\dfrac{1}{2}x+1=0\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-2^2}{2}=-2\)
Thay x=-1 vào (P), ta được:
\(y=-\dfrac{1^2}{2}=-\dfrac{1}{2}\)

1:
a: 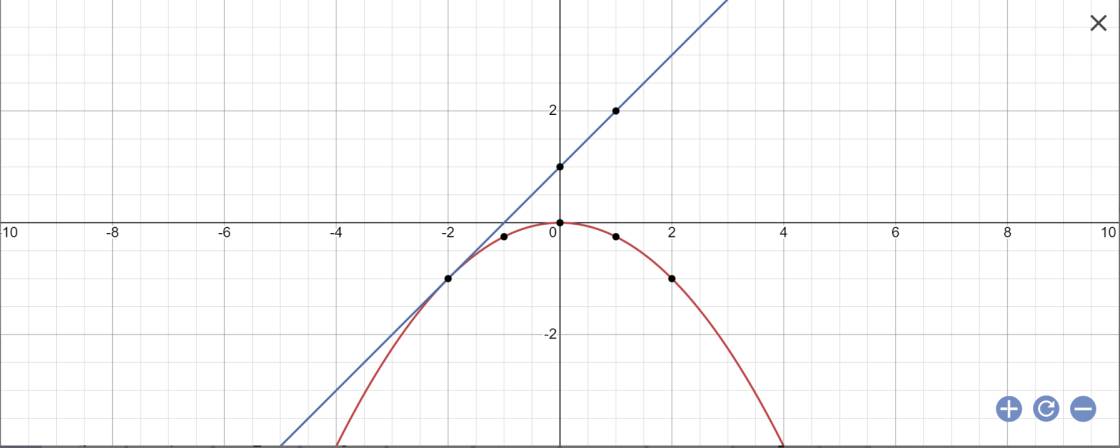
b: PTHĐGĐ là:
-1/4x^2-x-1=0
=>x^2+4x+4=0
=>(x+2)^2=0
=>x=-2
=>y=-1/4*(-2)^2=-1
2: 3x-y=5 và 2x+3y=18
=>9x-3y=15 và 2x+3y=18
=>11x=33 và 3x-y=5
=>x=3 và y=3*3-5=4
b: PTHĐGĐ là:
-1/2x^2=1/2x-1
=>-x^2=x-2
=>-x^2-x+2=0
=>x^2+x-2=0
=>x=-2 hoặc x=1
=>y=-1/2*4=-2 hoặc y=-1/2
a: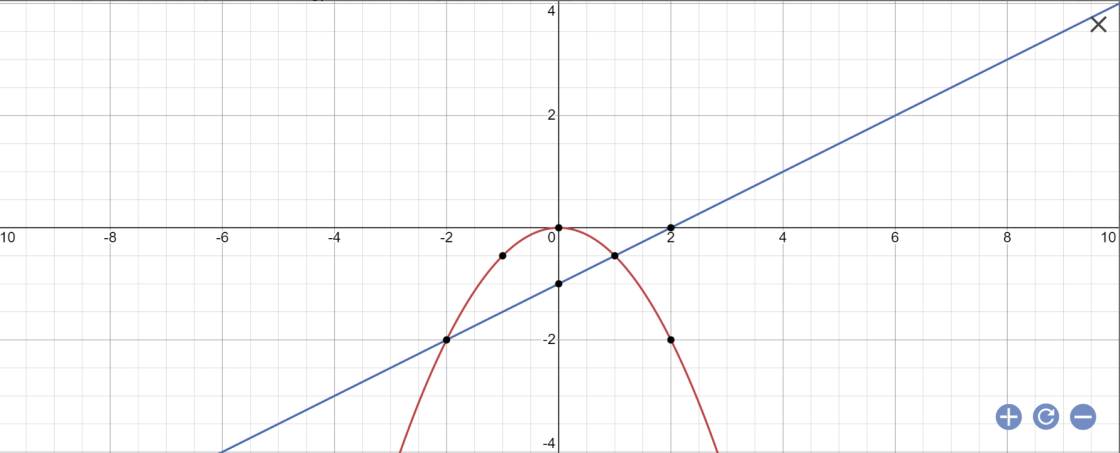
b. ta có phương trình hoành độ: 1/2.x^2=3/2.x-1 <=>1/2.x^2-3/2.x+1=0 <=> x^2-3x+2=0
Δ=1>0 =>pt có hai nghiệm phân biệt
x=2 =>y=2 =>A (2;2)
x=1 =>y=1/2 =>B(1;1/2)
Vậy (P)và (d) cắt nhau tại hai điểm A(2;2) và B(1;1/2)