Từ câu 04 đến câu 05.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2.
\(R=d\left(I;\Delta\right)=\dfrac{\left|3.2+4.\left(-1\right)-27\right|}{\sqrt{3^2+4^2}}=5\)
Phương trình: \(\left(x-2\right)^2+\left(y+1\right)^2=25\)
3.
- Với \(m=1\) pt trở thành: \(2=0\) (vô nghiệm) \(\Rightarrow\) thỏa mãn
- Với \(m\ne1\) pt đã cho vô nghiệm khi:
\(\Delta'=\left(m-1\right)^2-2m\left(m-1\right)< 0\)
\(\Leftrightarrow\left(m-1\right)\left(-m-1\right)< 0\Rightarrow\left[{}\begin{matrix}m< -1\\m>1\end{matrix}\right.\)
Vậy pt vô nghiệm khi: \(\left[{}\begin{matrix}m< -1\\m\ge1\end{matrix}\right.\)
4. Đặt \(AB=x>0\)
\(tan35^0=\dfrac{BC}{BD}=\dfrac{BC}{x+10}\)
\(tan40^0=\dfrac{BC}{AB}=\dfrac{BC}{x}\)
\(\Rightarrow\dfrac{tan35^0}{tan40^0}=\dfrac{x}{x+10}\Leftrightarrow x.tan35^0+10tan35^0=x.tan40^0\)
\(\Rightarrow x=\dfrac{10.tan35^0}{tan40^0-tan35^0}\Rightarrow BC=x.tan40^0=\dfrac{10.tan35^0.tan40^0}{tan40^0-tan35^0}\approx42,3\left(m\right)\)

3.
\(\pi< a< \dfrac{3\pi}{2}\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
b.
\(\dfrac{2+2cos2a-sin2a}{sin2a-sin^2a}=\dfrac{2+2\left(2cos^2a-1\right)-2sina.cosa}{2sina.cosa-sin^2a}\)
\(=\dfrac{4cos^2a-2sina.cosa}{sina\left(2cosa-sina\right)}=\dfrac{2cosa\left(2cosa-sina\right)}{sina\left(2cosa-sina\right)}=\dfrac{2cosa}{sina}=2cota\)
4.
\(\overrightarrow{BA}=\left(2;3\right)\Rightarrow\) đường thẳng d nhận (3;-2) là 1 vtpt
Phương trình d:
\(3\left(x-4\right)-2\left(y+1\right)=0\Leftrightarrow3x-2y-14=0\)
5.
Đường thẳng BC vuông góc đường cao kẻ từ A nên nhận (1;-1) là 1 vtpt
Phương trình BC:
\(1\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+3=0\)
C là giao điểm BC và trung tuyến kẻ từ C nên là nghiệm:
\(\left\{{}\begin{matrix}x-y+3=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow C\left(2;5\right)\)
Do M là trung điểm BC
\(\Rightarrow\left\{{}\begin{matrix}x_B=2x_M-x_C=-4\\y_B=2y_M-y_C=-1\end{matrix}\right.\) \(\Rightarrow B\left(-4;-1\right)\)
Do A thuộc đường cao kẻ từ A nên tọa độ có dạng: \(A\left(a;4-a\right)\)
Gọi N là trung điểm AB \(\Rightarrow N\left(\dfrac{a-4}{2};\dfrac{3-a}{2}\right)\)
N thuộc trung tuyến kẻ từ C nên tọa độ thỏa mãn:
\(2\left(\dfrac{a-4}{2}\right)-\left(\dfrac{3-a}{2}\right)+1=0\Rightarrow a=3\) \(\Rightarrow A\left(3;1\right)\)

1/
\(4FeS_2 + 11O_2 \xrightarrow{t^o} 2Fe_2O_3 + 8SO_2\\ SO_2 + 2H_2S \to 3S + 2H_2O\\ S + H_2 \xrightarrow{t^o,xt} H_2S\\ H_2S + 4Br_2 + 4H_2O \to 8HBr + H_2SO_4\\ H_2SO_4 + NaCl \xrightarrow{t^o} NaHSO_4 + HCl\\ MnO_2 + 4HCl \to MnCl_2 + Cl_2 + 2H_2O\\ 2Na +C l_2 \xrightarrow{t^o} 2NaCl\\ NaCl + AgNO_3 \to AgCl + NaNO_3\)
2/
\(S + H_2 \xrightarrow{t^o} H_2S\\ H_2S + \dfrac{3}{2}O_2 \xrightarrow{t^o} SO_2 + H_2O\\ 2SO_2 +O_2 \xrightarrow{t^o,xt} 2SO_3\\ SO_3 + H_2O \to H_2SO_4\\ CuO + H_2SO_4 \to CuSO_4 + H_2O\\ CuSO_4 + BaCl_2 \to BaSO_4 + CuCl)2\)
1)
4FeS2 + 11O2 -to-> 2Fe2O3 + 8SO2
SO2 + 2H2S -to-> 3S + 2H2O
S + H2 -to-> H2S
H2S + 4Br2 + 4H2O => H2SO4 + 8HBr
BaCl2 + H2SO4 => BaSO4 + 2HCl
2HCl-dp-> H2 + Cl2
Na + 1/2Cl2 -to-> NaCl
NaCl + AgNO3 => AgCl + NaNO3
2)
H2 + S -to-> H2S
2H2S + 3O2 -to-> 2SO2 + 2H2O
SO2 + 1/2O2 -to,V2O5-> SO3
SO3 + H2O => H2SO4
H2SO4 + CuO => CuSO4 + H2O
CuSO4 + BaCl2 => BaSO4 + CuCl2

\(1,\frac{-x}{15}=\frac{10}{25}\)
\(\Leftrightarrow\frac{-x}{15}=\frac{2}{5}\Leftrightarrow\left(-x\right).5=2.15\)
\(\Leftrightarrow\left(-x\right).5=30\)
\(\Leftrightarrow-x=6\Rightarrow x=-6\)
\(2,\frac{x+1}{14}=\frac{10}{35}\)
\(\Leftrightarrow\frac{x+1}{14}=\frac{2}{7}\)
\(\Leftrightarrow\left(x+1\right).7=2.14\)
\(\Leftrightarrow7x+7=28\)
\(\Leftrightarrow7x=21\)
\(\Rightarrow x=3\)
\(3,\frac{\left|x+2\right|}{26}=\frac{12}{39}\)
\(\Leftrightarrow\frac{\left|x+2\right|}{26}=\frac{4}{13}\)
\(\Leftrightarrow\left|x+2\right|.13=4.26\)
\(\Leftrightarrow\left|x+2\right|.13=104\)
\(\Leftrightarrow\left|x+2\right|=8\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=8\\x+2=-8\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=6\\x=-10\end{cases}}\)
Vậy x = 6 hoặc x = -10
\(4,x-\left(1\frac{1}{3}-\frac{2}{3}\right)=2\)
\(\Leftrightarrow x-\left(\frac{4}{3}-\frac{2}{3}\right)=2\)
\(\Leftrightarrow x-\frac{2}{3}=2\)
\(\Leftrightarrow x=2+\frac{2}{3}\)
\(\Leftrightarrow x=\frac{8}{3}\)
\(5,\frac{2}{5}:x-\frac{1}{5}=\frac{3}{5}\)
\(\Leftrightarrow\frac{2}{5}:x=\frac{3}{5}+\frac{1}{5}\)
\(\Leftrightarrow\frac{2}{5}:x=\frac{4}{5}\)
\(\Leftrightarrow x=\frac{2}{5}:\frac{4}{5}\)
\(\Rightarrow x=\frac{1}{2}\)
\(6,\frac{1}{2}.\left(3x-\frac{2}{5}\right)=\left(-3\right)^2\)
\(\Leftrightarrow\frac{1}{2}.\left(3x-\frac{2}{5}\right)=9\)
\(\Leftrightarrow3x-\frac{2}{5}=9:\frac{1}{2}\)
\(\Leftrightarrow3x-\frac{2}{5}=18\)
\(\Leftrightarrow3x=\frac{92}{5}\)
\(\Leftrightarrow x=\frac{92}{5}:3\)
\(\Rightarrow x=\frac{92}{15}\)





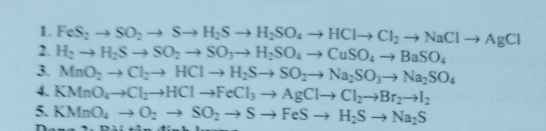
Bài 5 :
n Cu = a(mol) ; n Al = b(mol) ; n Mg = c(mol)
=> 64a + 27b + 24c = 11,5(1)
2Al + 6HCl $\to$ 2AlCl3 + 3H2
Mg + 2HCl $\to$ MgCl2 + H2
Theo PTHH :
n H2 = 1,5b + c = 5,6/22,4 = 0,25(2)
Bảo toàn electron :
2n SO2 = 2n Cu
2.0,1 = 2a (3)
Từ (1)(2)(3) suy ra a = 0,1 ; b = 0,1 ; c = 0,1
Vậy :
m Cu = 0,1.64 = 6,4 gam
m Al = 0,1.27 = 2,7 gam
m Mg = 0,1.24 = 2,4 gam